Determining the value of a transportation organization’s physical assets is important for both financial reporting and transportation asset management (TAM). In financial reporting, determining asset value is a fundamental step in preparing a balance sheet for financial statements to inform regulators and investors. For TAM, presenting data on the value of physical assets, such as pavement, bridges, and facilities, communicates what an organization owns and what it must maintain. Furthermore, information about asset value and how it is changing can help establish how the organization is maintaining its asset inventory and helps support investment decisions.
Calculating asset value for TAM is not simply good practice; it is also required of state Departments of Transportation (DOT) by Federal regulations. Title 23 of the Code of Federal Regulations (CFR) Part 515 details requirements for State DOTs to develop a risk-based Transportation Asset Management Plan (TAMP).
These regulations, initiated by the legislation Moving Ahead for Progress in the 21st Century (MAP-21), include a requirement for DOTs to calculate the asset value for National Highway System (NHS) bridges and pavement in their state. DOTs must also determine the cost required to maintain the value of their NHS assets.
To comply with the Government Accounting Standards Board (GASB) Statement 34, agencies also record their assets’ book value in annual financial reports. GASB 34 allows for either a standard (i.e., historic cost with straight-line depreciation) or modified approach. Many agencies struggle to reconcile financial asset valuation for GASB reporting with asset valuation for the purposes of asset management and the TAMP.
Reporting asset value is required in various documents, such as the financial reports of U.S. public agencies, which are prepared to comply with General Accounting Standards Board (GASB) Statement 34 (1), and National Highway System (NHS) transportation asset management plans. However, there are many nuances concerning how to perform the calculations, and a variety of different approaches has been used in the past for different applications.
Figure 1-1 depicts the value of an asset over time, and illustrates the different facets of the value calculation. The left side of the figure shows the value of the asset when it is first constructed or obtained. Over time the asset value tends to decline. The amount of value the asset loses, also called depreciation, represents the consumption of the asset’s benefits. If treatments are performed that extend asset life, such as rehabilitation, then the asset may regain some or all of its value. When the asset reaches the end of its life, it is valued at its residual value, also called salvage value.
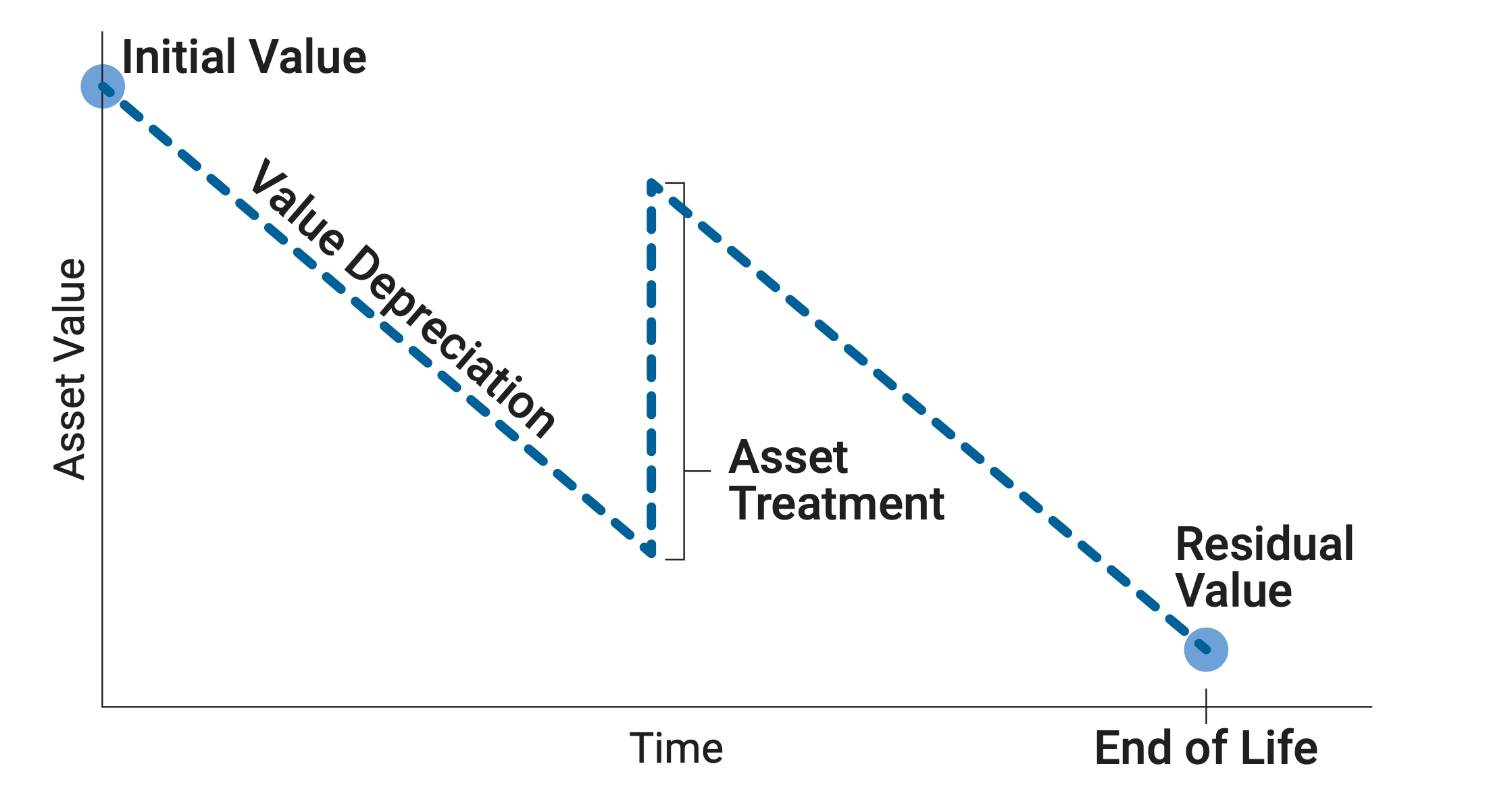
At each step of the asset value calculation illustrated in the figure, an analyst may choose how to perform the calculation. Specifically, he or she may use different approaches for calculating the initial value of an asset when first constructed or obtained, for establishing how value depreciates, for determining what treatments should be considered in the calculation and what their effects are, and for calculating residual value.
In truth there is no single correct way to calculate asset value, and there are good reasons why one may choose one approach over another or how much detail to incorporate into the calculation. The different approaches result from the fundamental considerations an analyst faces. These include:
- Different applications of asset value. The best approach for calculating asset value depends on how the valuation will be used. A private company may be interested in establishing fair market value of its assets to determine the profit to be gained by selling them. For public agencies, the primary purpose of financial reporting is to provide an accurate account of how the agency is spending resources to ensure the agency is financially sound and following regulations. In TAM, asset value supports decisions regarding investments to maintain and extend the life of assets. Another application of asset value is using it to understand the economic benefit or cost of the transportation system to society.
- Tension between simplicity and complexity. Often, improving a given approach to calculating asset value requires more data and/or more intensive calculations. For instance, straight-line depreciation is frequently used to determine asset value over time for the financial asset register. However, one can arguably obtain a more meaningful and useful estimate of depreciation for TAM applications by utilizing data on asset condition to establish asset value for the technical asset register. In these situations, it is important to balance the desire for a more accurate calculation with the benefit of having a simple, repeatable, and sustainable approach.
- Limits on what a single measure can provide. Once calculated, the value of an asset provides a powerful and compelling measure. Yet no single number, however well-conceived, is sufficient for conveying all of the information one may wish to communicate regarding an asset. Thus, a valuation approach should be adapted so that it provides the information of greatest use in decision-making. For instance, an agency may wish to tailor the calculation such that annual depreciation approximates the cost to maintain asset value. However, this limits the ability to use the change in asset value in other ways, such as for showing how a proactive preservation strategy could be more cost-effective than a reactive strategy.
The objective of this guide is to provide step-by-step guidance for calculating asset value in support of asset management applications. It describes an approach to calculating value that includes six basic steps, offering alternative approaches for each step to account for the considerations described above, as well as for differences in the scope of the calculation, available data, and other factors.
It is important to note that while the guidance presented here is intended to be consistent with best practices in public sector accounting, this document is not intended as an accounting standard or as a guide for calculating asset value in support of agency financial reports. Several accounting standards exist for valuing assets to support financial reporting that do address these topics. The predominant standard for U.S. public agencies is the aforementioned GASB Statement 34 (1), and its international counterpart is the International Public Sector Accounting Standards (IPSAS). IPSAS standards are based on standards of the International Accounting Standards Board (IASB), particularly International Accounting Standard (IAS) 16: Property, Plant and Equipment (2) and International Financial Reporting Standard (IFRS) 13: Fair Value Measurement (3). International Standards Organization (ISO) 55002 asset management standard (4) discusses additional important concepts for relating asset value to asset management, such as the distinction between value generation and value determination. While important to the industry and general understanding, these standards are not the focus of this guidance.
The recently-updated ISO55002 standard discusses the differences between value generation, the benefits from use or ownership of assets defined as “value from”, and value determination, an asset’s valuation for purposes of sale defined as “value of.”
Using a rental car company as an example, rental vehicles lose sale value (“value of”) immediately after purchase, but the company continues to generate value (“value from”) by renting their cars to users. The rental car company is then able to make a profit from assets which are losing value. In traditional business cases, asset owner investment decisions are more often guided by “value from” than “value of.”
This guidebook consists of nine chapters, a glossary and additional technical appendices. The first two chapters, including this one, introduce the content and key concepts. Chapters 3 to 8 provide step-by-step guidance for calculating asset value. Chapter 9 provides a set of worked examples of the calculations.
The contents of the remaining chapters are as follows:
- Chapter 2 – Asset Value Overview introduces the concept of asset valuation. It defines asset value from the cost, market, and economic perspectives, identifies applications of asset value for supporting TAM, and presents the simplified steps for calculating asset value. The chapter concludes with a summary of U.S. and international accounting standards and their underlying assumptions.
- Chapter 3 – Asset Valuation Scope outlines the different factors one should consider when establishing their asset valuation calculation approach. This includes selecting which assets and systems to include in the calculation, reviewing available data, and determining the level of detail at which the calculation will be performed, and specifically whether to break complex assets into components.
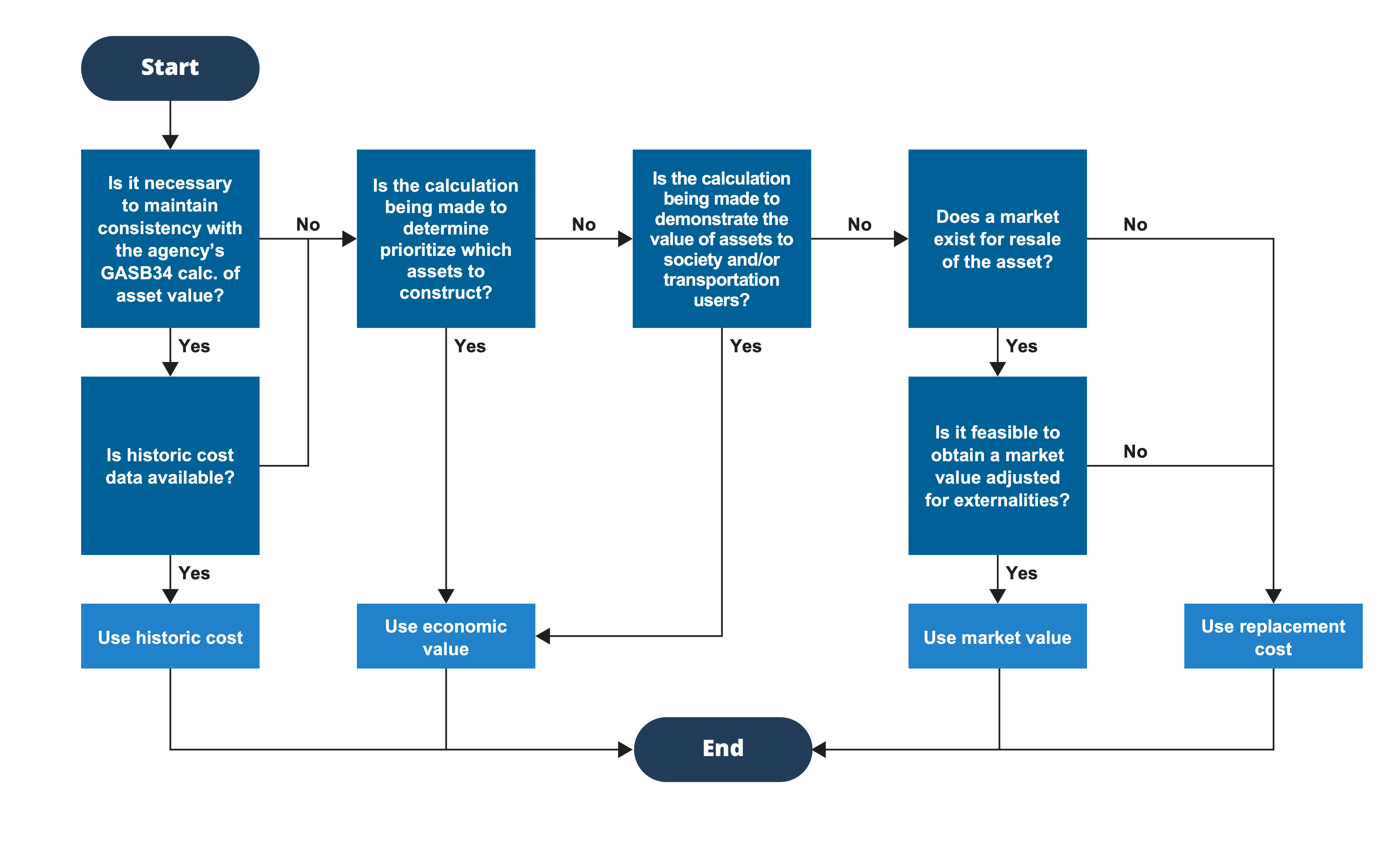
- Chapter 4 – Initial Asset Value describes how to calculate the initial value of an asset when it is first constructed or obtained. The chapter describes four basic approaches to performing the calculation reflecting different perspectives on asset value: historic cost, replacement cost, market value, and economic value.
- Chapter 5 – Treatment Effects identifies and defines which treatment effects should be included in the asset value calculation. It discusses treatment costs, treatment effects, and the concept of residual value.
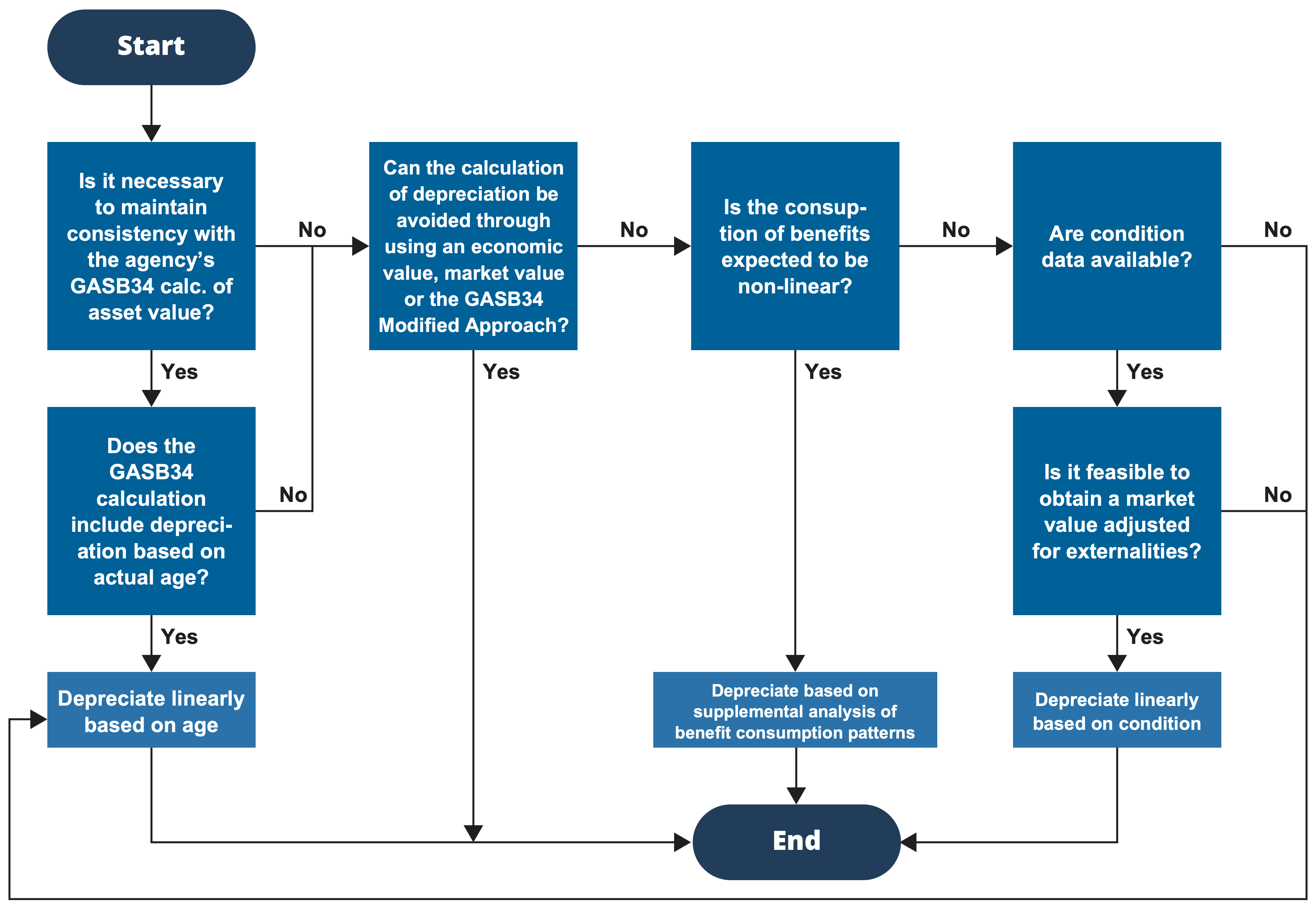
- Chapter 6 – Depreciation describes how to calculate the loss in value of an asset over time. The chapter describes three basic approaches to calculating depreciation. Each approach focuses on a different basis for depreciation: asset age, condition, or the pattern of benefit consumption for the asset.
- Chapter 7 – Measure Calculation brings together all of the steps from Chapters 3 to 6 to calculate the overall asset value. Also, it describes how to calculate additional supporting measures, such as the cost to maintain value, asset sustainability ratio, net present value, asset renewal funding ratio, and asset consumption ratio.
- Chapter 8 – Using Asset Value to Support TAM Decisions addresses the interpretation, communication, and application of asset value. It explains how to test different treatment scenarios using asset value, and it clarifies when and how asset value can support prioritization. The chapter also explains when and how to use sensitivity analysis to understand the asset value results.
- Chapter 9 – Case Studies presents a set of case studies undertaken to demonstrate the process outlined in this guide. The case studies illustrate scenarios for calculating and applying asset value from a range of different agencies and asset types.
This guide is intended for use by public agencies seeking to calculate asset value in support of TAM and TAM decisions. This includes, but is not limited to, applications such as:
- Using asset value to communicate the extent of assets an agency owns or maintains;
- Reporting asset value in a TAMP;
- Determining how value is expected to change over time given an agency’s investment strategy;
- Calculating the cost to maintain asset value; and
- Evaluating the impact of different treatment options on the value of a given asset or asset class.
This guide is designed for use by all U.S. public agencies managing transportation assets, including state and local DOTs, transit agencies, port authorities, airport operators, and others. Key users of the guide include engineers, planners, and analysts charged with managing transportation assets, calculating asset value, and/or helping support investment decisions. The guidance may also be useful for accountants and financial analysts responsible for agency accounting and financial reporting for purposes such as comparing TAM asset value calculations to those developed for financial reports or other applications.
The guide is designed to support a variety of different uses; it offers an explanation of essential concepts, step-by-step guidance, examples, and different levels of maturity in applying the guidance. These applications are discussed below.
Basic Overview of Asset Value and Related Concepts
Each chapter provides an overview of key concepts that help develop an understanding of the subject matter. Chapter 2 introduces concepts related to calculating asset value. Chapter 3 discusses key considerations involved in calculating asset value. In Chapters 4 to 8 the first section of each chapter further details concepts important for applying the guidance in the chapter. For additional information on TAM concepts, the reader should refer to the American Association of State Highway and Transportation Officials (AASHTO) TAM Guide (5) and National Cooperative Highway Research Program (NCHRP) Report 898: A Guide to Developing Financial Plans and Performance Measures for Transportation Asset Management (6).
Step-by Step Guidance
Chapters 3 to 8 provide step-by-step guidance for calculating asset value. Each chapter describes the options an agency has in determining how to calculate asset value at each key decision-point. These chapters include flowcharts to assist the decision-making process, such as determining how to calculate the initial value of an asset and how to calculate depreciation.
Practice Examples
There are numerous practice examples in each chapter of the Guide. Chapter 3 offers examples from other agencies illustrating the typical scope selections and their impacts on the valuation. Chapters 4 to 8 include examples of how different agencies have addressed issues discussed in the guidance. Chapter 9 details a set of worked example walking through the asset value calculation from beginning to end.
Practice Assessment
Chapters 4 to 8 each include a section titled “Practice Assessment.” This section provides examples of “emerging”, “strengthening”, and “advanced” practices with respect to different aspects of the asset value calculation. All of the practices described illustrate how the guidance can be applied, albeit with varying levels of complexity. In this context, an emerging practice is one that supports the guidance with minimal complexity, an advanced practice illustrates a “state of the art” example in which an agency has addressed some aspect of the asset value calculation in a comprehensive manner, and strengthening practice lies between these two extremes.
Note that the labels applied to the practice examples is designed to be consistent with the maturity scale used in the AASHTO TAM Guide. This resource describes additional tools and approaches for assessing TAM maturity.
Knowing what a physical asset is worth – its value – can be very useful both for financial reporting and for supporting asset management. Even if the notion of asset value is somewhat abstract, an asset owner generally prefers that the value of their assets increases or at least remain constant over time. Fundamentally, tracking and reporting asset value helps a transportation agency monitor the state of its assets and provides a sense of whether the inventory is improving or in a state of decline. Transportation agencies use data on asset value in a variety of ways to support asset management. Major applications of asset value aiding an overall asset management program are described below.
Asset value is used to communicate what assets an agency owns, their extent, and the agency’s responsibility for maintaining the asset inventory. Each asset has its own unit of measure: pavements may be summarized in terms of lane miles, bridges in terms of deck area, and other assets in terms of a count. However, it can be hard to relate these different units and to summarize their asset portfolio as a whole. For instance, how does one lane mile compare to 1,000 square feet of bridge deck or 100 culverts?
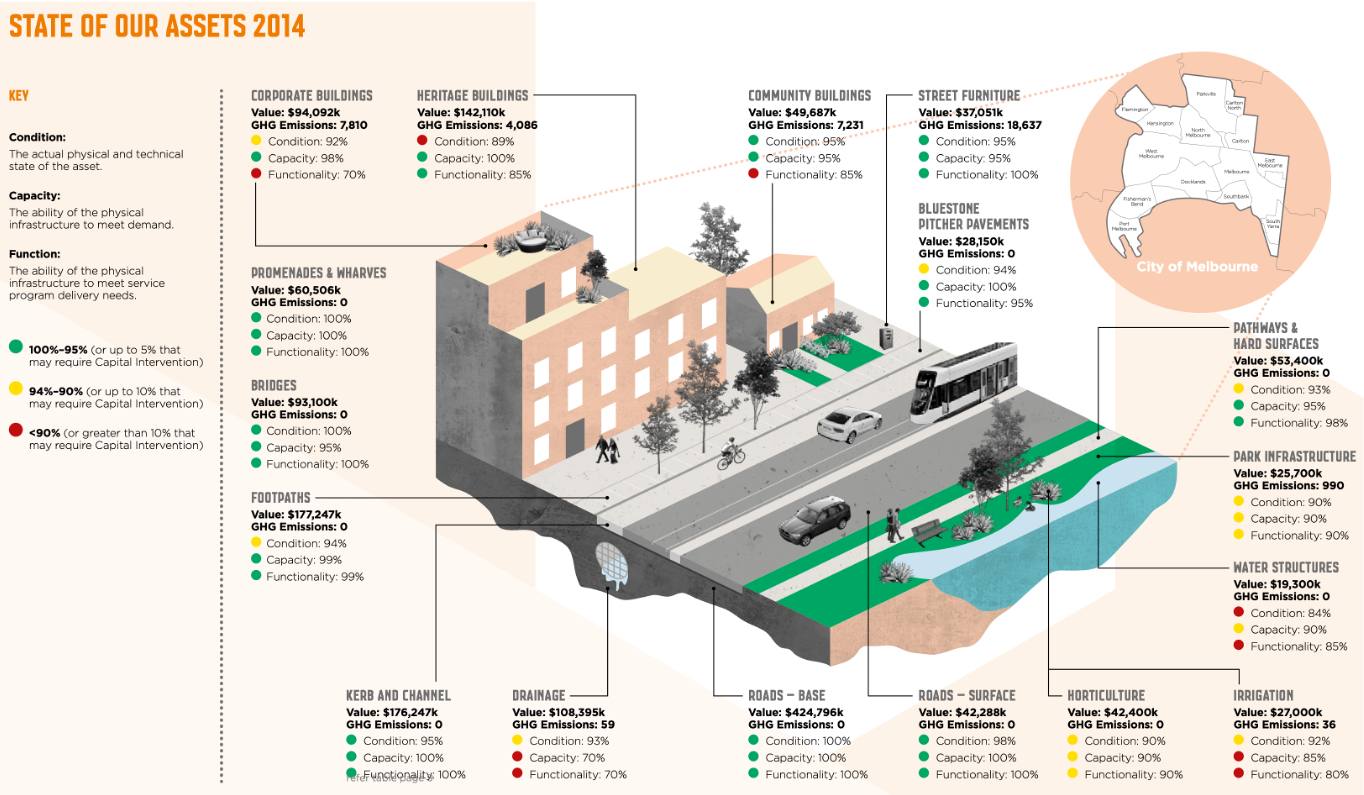
Figure 2-1, reproduced from the Melbourne Asset Management Plan (7), depicts the assets owned by the agency, including the roadway surface, roadway base, bridges, footpaths, drainage, buildings, and various other assets. Each type of asset is illustrated and labeled with its value and annual greenhouse gas (GHG) emissions. The City of Melbourne uses these two numbers to communicate the state of their assets to the public and other stakeholders.
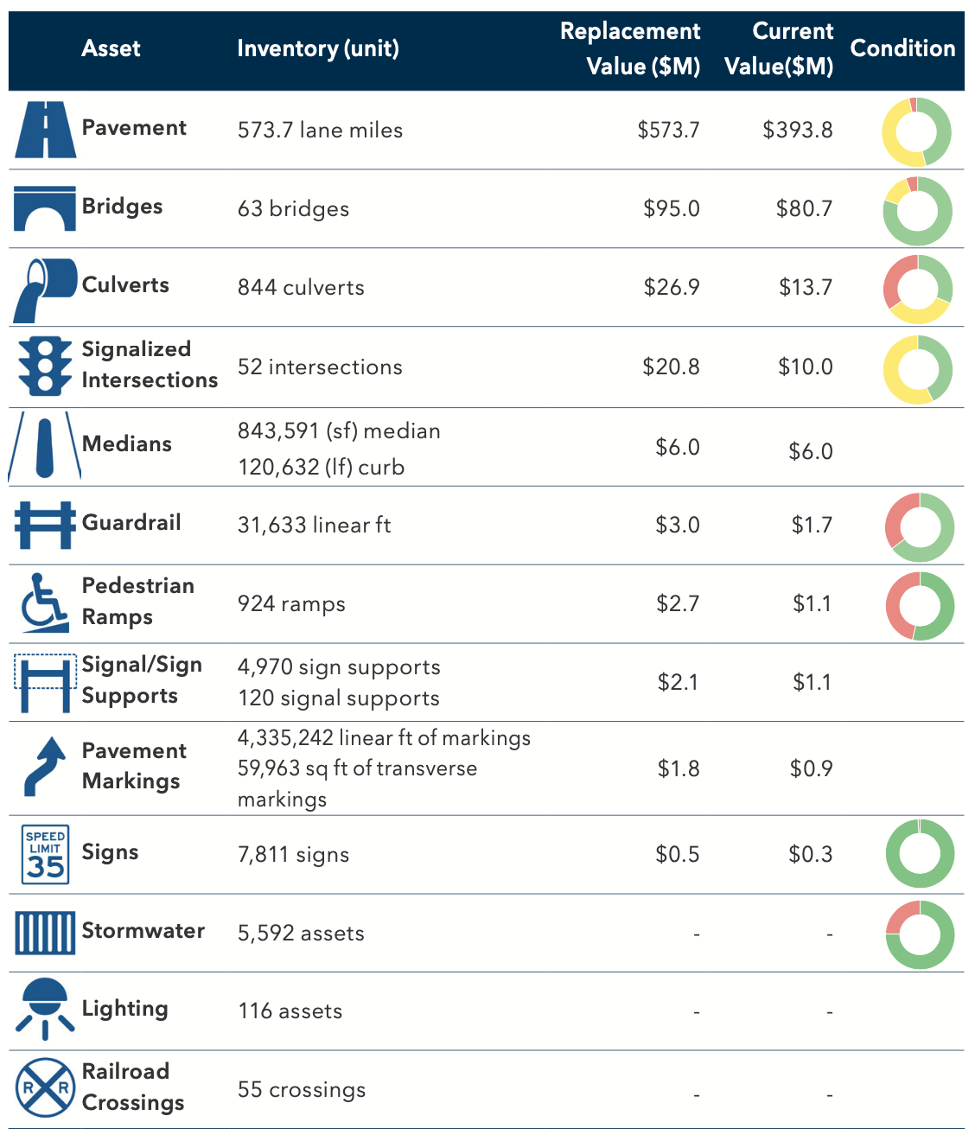
Figure 2-2 shows an example from the TAMP prepared by Carver County, Minnesota (8). Here asset quantities and conditions are summarized for 13 transportation asset classes. Asset replacement value and current asset value are shown for the ten asset classes for which Carver County Public Works is responsible. The two asset values help communicate the state of the county’s assets to the public as well as providing a financial account of the publicly-owned assets.
Various measures have been formulated that use asset value and changes in value to demonstrate that an agency is managing its assets responsibly. The basic premise is that as assets deteriorate or depreciate in value, an agency should invest to maintain their value. Public agencies in Australia and New Zealand have used asset value in this manner for over a decade. The Australian Infrastructure Financial Management Manual (AIFMM) details recommended measures and practices for monitoring and applying asset value (9). A key measure in Australia is the Asset Sustainability Ratio (ASR), or ratio of spending on asset renewal and replacement to annual depreciation.
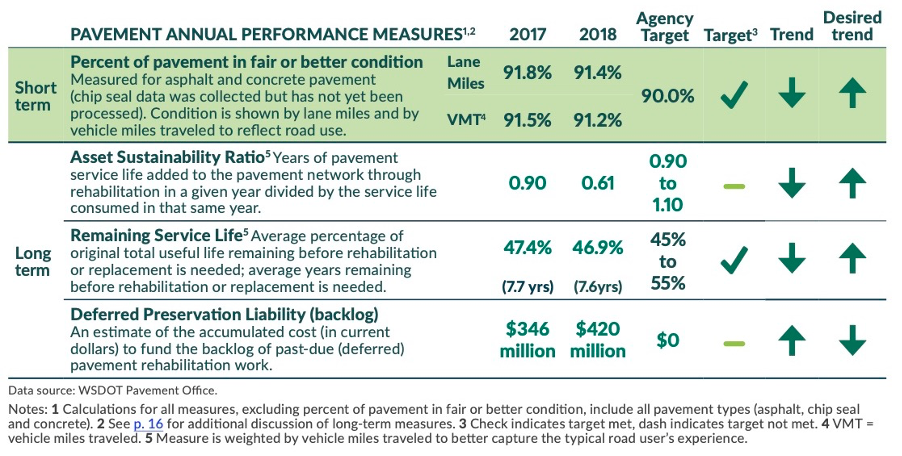
In the U.S., several agencies have calculated similar measures. Figure 2-3, reproduced from the Washington State Department of Transportation (WSDOT) Gray Book (10) includes several long-term measures for pavement assets related to asset value. The Gray Book is a quarterly performance report which covers a variety of aspects related to WSDOT’s transportation system and assets. The Gray Book from the fourth quarter of 2019 includes the following long-term measures for pavement: ASR, Remaining Service Life (RSL), and Deferred Preservation Liability (backlog). In this case, ASR is calculated as the years of pavement life added through different treatments divided by life consumed.
Asset value can be used to help illustrate the difference between alternative investment strategies, such as when comparing a strategy of performing recommend preservation treatments on an asset over its life to an alternative strategy in which preservation treatments are deferred, resulting in worse relative condition and potentially a shorter asset life.
One way to compare different investment strategies for a given asset is to perform a life cycle cost analysis (LCA). In such an analysis, the costs for an asset are computed over time for a given scenario relative to a base case. A results of a given investment strategy can be summarized by calculated the net present value for the strategy, where NPV is the sum of the discounted benefits of the asset less the sum of discounted costs.
Asset value is potentially relevant to such an analysis in two ways. If one adopts an economic interpretation of asset value, as discussed further in the next section, NPV can serve as the definition of asset value. However, even when asset value is computed differently from NPV, it can be used to represent the residual value of the asset at the end of the analysis periods. This provides a way to compare investment scenarios that result in different condition and/or remaining
asset life.
Another potential application of asset value for supporting TAM is helping compare and understand asset investment options. While asset value alone is insufficient for prioritizing investments, when used in conjunction with life cycle cost analyses it can provide a complete view of the asset’s worth. In particular, asset value can help prioritize decisions such as:
- Resilience investments;
- Reconstruction; or
- Decommissioning
Asset value provides insights for assets identified for decommission or reconstruction by pitting their intrinsic value (including the replacement cost and socio-economic importance) against the costs necessary to maintain or replace the asset. Asset value also supports investment decisions for resilience investments by placing an emphasis on the importance of asset renewal to mitigate future risks and by directly accounting for the potential costs associated with a risk.
In these applications, asset value is defined broadly, considering the cost of constructing the asset and its value to road users and society. For example, in determining which bridges to focus on for a set of resilience investments, one might consider the cost of replacing or improving each bridge, the risk to the bridge as a result of flooding or other events, the level of service the bridge provides, and the impacts to mobility in the event the bridge is closed. The inclusion of asset value in the investment decision could lead to the renewal of the asset to withstand the risks, or it could suggest an asset should be allowed to fall into obsolescence. Either way, it provides context to the investment decision.
Thus far, we have discussed how asset value can be used to support TAM but not what it actually represents. This begs the question, what is asset value? According to the definition established by Organisation for Economic Co-Operation and Development (OECD), in its report Measuring Capital (11), a physical asset has no intrinsic value. Instead, its value results from the benefits it yields, be they to the asset owner, a set of transportation system users, society as a whole, or some combination thereof. As an asset ages, it depreciates, or loses value, when its benefits are consumed.
Speaking generically about capital and its value, OECD discusses that capital has a dual nature; it serves both as a means to store wealth and as a source of capital services. OECD further discusses the different perspectives on asset value as well as the fact that the best perspective depends on one’s “analytical purpose.”
Asset Value: the discounted stream of future benefits that the asset is expected to yield.
Depreciation: loss in the value of an asset as it ages, equivalent to the consumption of fixed capital.
Source: OECD, Measuring Capital (11)
Figure 2-4 illustrates the different perspectives on transportation asset value, adapting concepts from the OECD discussion. The figure illustrates three perspectives: a market perspective, a cost perspective, and an economic perspective. Each perspective is discussed further below.
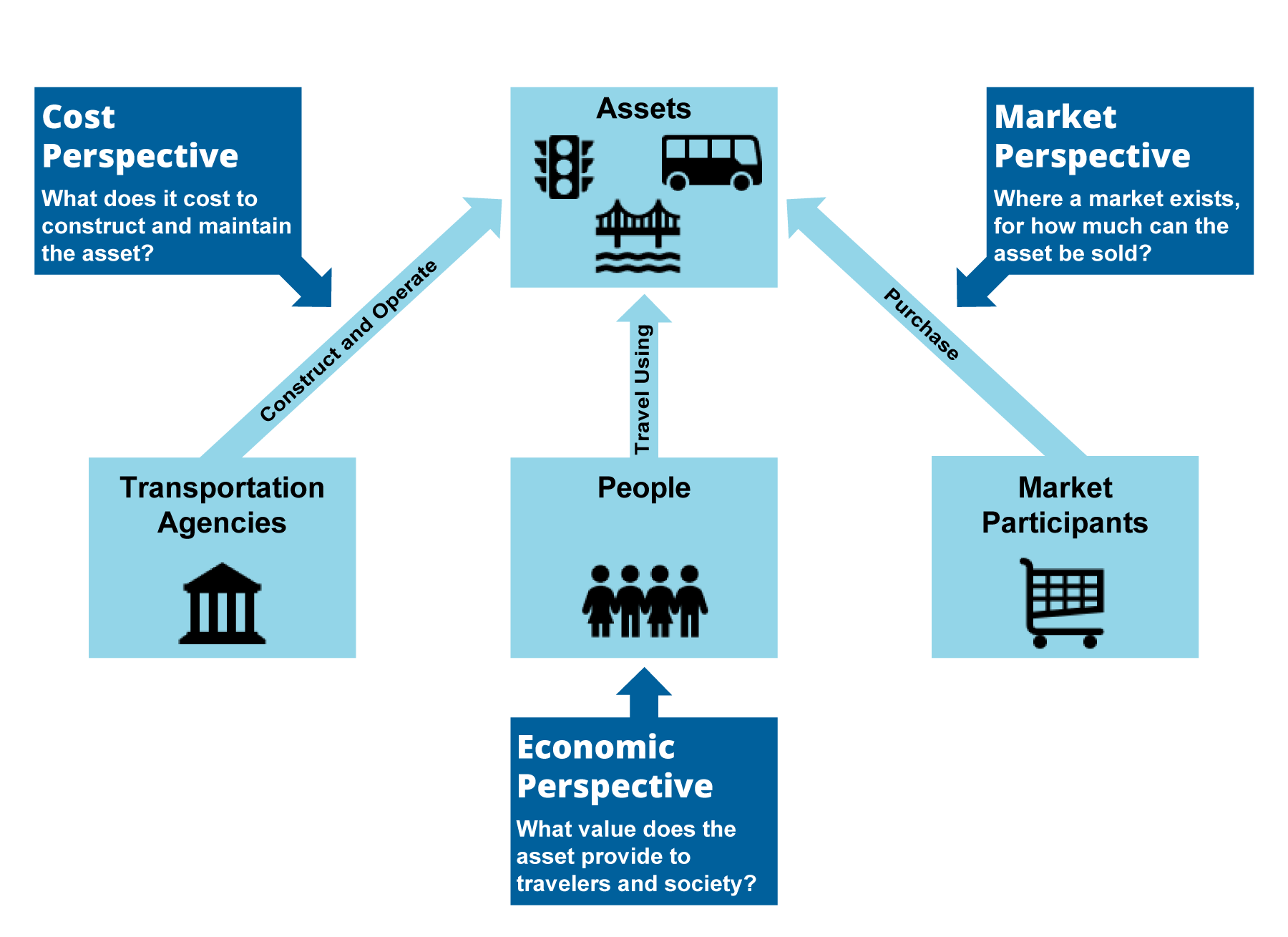
The cost perspective focuses on capital costs incurred by the asset owner. When establishing value from this perspective one asks: “How much does it cost us to acquire this asset and operate it over time?”
In cases where a competitive market exists for an asset, the cost and market perspectives yield the same result for the initial value of an asset; the cost is notionally the price of the asset on the market. However, this perspective still yields a value in cases where no market exists, or where the market is not competitive. Even if there is no market for an asset, there is still a cost incurred in purchasing, constructing, and operating the asset over time.
One important consideration in adopting the cost perspective is to establish whether to use historic or current costs. The historic cost of an asset is the cost that was actually paid for the asset. The current cost is the cost of replacing the asset in today’s dollars, regardless of what was actually paid in the past. GASB Statement 34 specifically requires agencies to report the historic costs of asset purchase or construction, as is consistent with U.S. Generally Accepted Accounting Principles (GAAP). U.S. GAAP emphasize the use of conservatism, or avoiding the overstatement of net assets and income. Thus, U.S. agencies must report asset values using historic costs or estimated historic costs in their financial reports to be consistent with either method in GASB 34, even if they calculate value in other ways to support TAM.
For supporting TAM, and for financial reporting outside the U.S., asset owners tend to use the asset’s current replacement cost in today’s dollars rather than the asset’s purchase price. The use of the current replacement cost is recommended for calculating the fair value of an asset as defined in IFRS Number 13. This cost is used as a proxy for the price that would be charged for the asset in the event that a market existed. Also, it is the cost that is most relevant to an asset manager trying to make investment decisions that involve spending money in today’s dollars.
The basic issue with the cost perspective is that it leaves no daylight between cost and value; these are one and the same. If one asks what value will be derived from spending $1 million to reconstruct a road, from the cost perspective the answer is “$1 million, of course.” Consequently, the cost perspective can help answer questions about how best to manage assets, but it is ill-suited for addressing questions concerning the underlying value of transportation assets to society. For answering such questions, one must instead turn to the economic perspective.
The market perspective focuses on the price of an asset on the open market. When establishing value from this perspective one asks: “For how much can an asset be sold on the market?” For example, when valuing an automobile one might seek to determine the resale value should the car be sold through an auction or to a reseller.
The virtue of this perspective is that it leverages the behavior of free markets to determine how much value an asset is expected to yield in the future. If the market for an asset is competitive, then the asset’s market value should theoretically account for the future benefits provided to the buyer. After all, nobody would want to purchase an asset at a cost greater than its expected benefit. The competitive nature of the market should ensure that no asset is sold at less than this value. Thus, this perspective is extremely valuable where a well-defined market exists for an asset.
The challenge with adopting this perspective is that it can be hard to identify a market, let alone a competitive one, for many types of transportation assets. Markets typically exist for assets that are manufactured and can be readily exchanged between different parties, including many types of vehicles, equipment, facilities, and land. Fixed assets, such as the roads and bridges necessary to provide mobility to society, are not particularly mobile themselves, and they do not lend themselves to being resold once constructed because they do not generate revenue. Markets can exist for toll roads and bridges, but it is important to note that the prices in these markets may not be wholly indicative of the asset’s condition, as they typically involve the leasing, not the sale, of an asset for an allotted period of time. Also, the market price does not account for externalities – costs and benefits placed upon others and not perceived by the buyer. An example of a positive externality is the support of emergency services such as ambulances; negative externalities include items such as air pollution, congestion, and noise. Depending on the application, it may be necessary to adjust the market price for externalities.
One approach for calculating a market value for fixed assets is to examine cases in which infrastructure has been privatized, such as where a private firm bids to own, operate, and maintain a highway. The asset value considerations and applications for private infrastructure are explored further in Chapter 4. For now, to use this as the basis for establishing value for other assets one must ask:
- To what extent can the price of a given privatization contract or other transaction be generalized to other transportation assets? For instance, it may not be reasonable to apply the value of a specific toll road to other non-toll roads and bridges. These assets’ risks, costs, and revenues depend on unique characteristics, such as the length of the contract or local traffic flow, which are not easily generalized or tracked.
- Does the market price account for the full range of benefits and externalities? In the example of a toll road, one can use the transaction price to determine the value of future tolls for a specific road. However, this does not account for impacts of traffic diverted to or from other roads as a result of the toll road, changes in consumer surplus to road users being tolled, environmental impacts, and a host of other issues.
- Is the market competitive? Certainly, a public agency awarding work always seeks a competitive market, but in large, high-cost bids there may be a small number of bidders, and it may be difficult to establish whether a competitive market actually exists. If the market exists but it not competitive, then it is possible to establish a market price, but it may be a different price than that of a truly competitive market.
However it is established, the market value of an asset is viewed as the best representation of asset value based on international accounting guidance. Based on the IFRS 13 standard, the fair value is the price that would be set for an asset in a market, in the event one existed, regardless of whether such a market actually exists. Where no such market exists, IFRS 13 describes using the cost of the asset as a proxy, consistent with the cost perspective.
Fair Value: the price that would be received to sell an asset or paid to transfer a liability in an orderly transaction between market participants at the measurement date.
Source: IFRS, Standard Number 13: Fair Value Measurement (3)
The economic perspective focuses on the benefits generated by an asset. When establishing value from this perspective one asks: “What are the benefits of the asset to travelers and society?” In general guidance for asset value (11, 12), this perspective is also called the “income perspective”, as it involves calculating the income generated by an asset.
The valuation of an asset is a fundamental area of economic analysis, especially in the context of a benefit-cost analysis (BCA) conducted to determine whether improvements to an asset are worthwhile. When conducting a BCA, one determines the cost of an investment as described above for the cost perspective and calculates economic benefits by observing the choices people make to infer the value they derive. Transportation facilities do not intrinsically generate value. Instead, value is generated when a facility is used to transport people or goods. Analysis of the different values incorporates forecasts of roadway uses, which are typically obtained from travel demand models that frame transportation choices through a nested set of decisions, including whether or not to take a trip, and if the trip is taken, which destination, mode, and route is chosen. Since operating a wide network of roadways expands transportation choices, and thus the implicit value of exercising an option to travel, a fundamental purpose of asset management is to maintain existing facilities so that their use generates value.
The cost, market, and economic perspectives on asset value differ in subtle and important ways. For example, a cost perspective generally starts from an implicit assumption that a facility is worth maintaining at the level of service for which it was originally planned and constructed. The actual use of the facility does not factor into the assessment except when it is used to indirectly estimate the rate of deterioration and maintenance schedule. In comparison, the market approach directly considers the value of the facility to users in addition to the cost to maintain it. The market approach can be considered from the perspective of a concessionaire who could evaluate the facility based on their opportunity to recover their cost and earn a profit, through revenue collection. Accordingly, the number of users and their willingness to pay for using the facility are key determinants of value. Note also that this willingness to pay is typically associated only with users’ potential for saving time or out-of-pocket costs.
In contrast, an economic measure of asset value stems from a more comprehensive value, based on the use of a facility. Economic asset valuation is an analytical exercise that establishes a rationale on whether and when a facility ought to be constructed or improved. Academic literature and practitioner-oriented documents and guidelines discuss two ways in which a transportation facility provides economic value (13, 14). A user-based measure of value draws directly from separable and additive accounting of key benefit categories, such as travel time, out-of-pocket expenditures, accident risk, pollutant externalities, and pavement maintenance, and some potential site-specific impacts that arise from facility use or location. Alternatively, where transportation facilities lower the cost of mobility, they can induce more productive investments in capital and labor, key measures of gross domestic product (GDP), and a macroeconomic indicator of transportation value. There are various challenges in linking economic benefits to specific changes in GDP. The approach presented here addresses the economic benefits of transportation assets without making an explicit linkage between these benefits and GDP.
There are several important dimensions in a user-based, economic valuation of transportation assets that one must consider when valuing assets from an economic perspective. These include the following:
- Relative value. Since a transportation facility has no intrinsic value (beyond its use), economic valuation of an existing facility constructs a counterfactual case (e.g., an alternative design, route or mode) for comparison with current conditions. Depending on the asset management context, several different types of alternatives could be established for comparison.
- Measures of value. Transportation investment has a number of different impacts both positive and negative. A variety of different measures are needed to quantify the value from an investment. These include, but are not limited to, travel time savings, vehicle operating costs, crash costs, emissions costs, costs from environmental impacts, changes in property value, and agency costs.
- Consideration of the stream of costs and benefits. The time span over which asset value is measured creates complexities since many roadways are already or will become long-lasting corridors that communities develop around. The present value of a facility’s future uses must be determined, and this is directly determined by a discount rate intended to reflect the present value decision-makers place on any future uses.
- Changing contexts. It is not enough to manage assets assuming current valuation conditions will remain in perpetuity. For example, the value of a transportation asset may change if policy perspectives shift toward free-access facilities versus revenue-generating ones or if climate conditions render facilities more vulnerable to extreme events.
Each asset value perspective emphasizes a specific aspect of how transportation assets are constructed and utilized. All three perspectives are valid, and can provide insights that help communicate information about assets and support decision-making.
While each of the perspectives supports some of the applications described in Section 2.1, many public agencies rely on the cost perspective for their calculation of asset value. The cost perspective helps an agency directly relate its expenditures on assets to changes in their value, and it supports a large number of TAM-related applications. Also, where a market exists, the cost of replacing the asset, depreciated based on its age or use, tends to correlate closely to its price. Where no market exists, the depreciated replacement cost serves as a proxy for its market price.
Regarding the relationship between the cost and economic perspectives, the cost of an asset does not provide direct insight into the economic benefits generated by an asset, and cannot support decisions that rely on this information. However, if one assumes that an existing asset is worthy of maintenance, the expectation is that its benefits over time must at least equal, and may greatly exceed, its replacement cost. Further, whatever the benefits may be to transportation users and society, those benefits will continue to accrue provided the asset remains in service. Thus, for many TAM applications it is sufficient to focus on the cost to the agency of keeping the asset in service through efficient maintenance and planning, with the assumption that doing so is inherently worthwhile.
This section outlines the basic steps in calculating asset value. Though they are intended to support the different applications described in Section 2.1, the steps are the same regardless of the specific application, and regardless of which perspective described in Section 2.2 one assumes. The steps explicitly acknowledge the different applications and perspectives, and they walk the analyst through the key decisions for calculating asset value. Figure 2-5 summarizes the steps to calculate asset value, and the following subsections describe each step further.

Define the Analysis Scope
The first step is to determine the scope of the analysis. Here, one must determine the assets for which they will calculate value, and the level of detail at which the calculations will be performed. The selected approach depends upon the intended application of the asset value calculation.
When deciding which assets to incorporate, one must consider both the specific asset classes and the systems or networks included in the analysis. For example, to comply with Federal requirements for TAMPs, State DOTs must calculate asset value for two asset classes – pavements and bridges – under one system – the NHS.
All asset classes identified in the requirements should be included in the calculations, and no asset should be included in multiple classes. However, when calculating the value for pavement, one must decide if this includes the value of shoulders, guardrails, signs and traffic signals, and Intelligent Transportation Systems (ITS). Ideally, the decision of what asset types to include is supported by a review of a comprehensive asset register and a consideration of the available data.
The level of detail required for the analysis is a function of the intended applications of the asset value calculation and the availability of data. In concept, the level of detail should be sufficient for specifying the impact of different treatments considered in the calculation, though this topic is discussed further in Step 3 – Determine Treatment Effects. Ideally, one should include treatments that add life to an asset and analyze assets at a level of detail that accounts for treatment effects. For instance, it may be necessary to consider major components of a bridge (deck, superstructure, substructure) separately in the analysis, given these components have different lifespans and some treatments may extend the life one component but not another (e.g., deck replacement or substructure repair).
Establish Initial Value
Once the analysis scope has been established, the next step is to decide how to calculate the initial value of an asset. This step accounts for the different applications and perspectives of asset value.
For many TAM applications, the preferred approach is to establish the initial value based on the asset current replacement cost in today’s dollars. As discussed in Section 2.2, this approach supports decisions regarding how an agency should spend its available budget on its assets. This approach tends to be the most straightforward to implement, and it is recommended as a default.
However, for certain applications it may be preferable to use an alternative approach to establish asset value. For U.S. agencies that seek to maintain consistency with their approach to financial reporting, it may be necessary to establish initial value based on purchase price, consistent with GASB 34. For applications that involve considering which assets should be constructed or maintained, an economic perspective may yield a more defensible result. Where market value is available, this is usually preferable, particularly given the ease of calculation relative to other approaches.
Determine Treatment Effects
Another important step in calculating asset value is determining treatment effects. Here, one must establish what treatments will be explicitly considered in the analysis, treatment costs, the assets that a treatment impacts, and the effects of treatment. Depending on the depreciation approach, one may specify treatment effects in terms of change in asset life or change in asset condition (which can then be converted to a change in effective life).
The major question to answer in this step is what treatments to consider. At a minimum one should consider asset replacement or reconstruction, and the treatments identified in an asset’s life cycle analysis should be reviewed as well. Frequently, it is necessary to consider other treatments short of replacement or reconstruction to support TAM applications. For example, when trying to demonstrate the value of performing preventive maintenance activities for pavement, one approach is to show how asset value for a representative pavement section changes over time with and without preventive maintenance.
Once the treatments are established, one must specify treatment costs, what assets or asset components are addressed by a given treatment, and the effects of treatment on asset or component life or condition. Treatments that are assumed to occur but not explicitly considered should be reflected in estimates of asset life; preventive maintenance activities often fall within this category. For instance, an estimate of the life of a new pavement should assume preventive maintenance treatments occur as scheduled.
Establish Depreciation Approach
Depreciation is necessary when calculating how asset value changes with time. Any asset with a finite life loses value over time. As in the case of calculating initial asset value, there are many different approaches to calculating depreciation. The best approach to use depends on the intended application of the calculation, one’s perspective on what value represents, and the data available to support the calculation.
While depreciation tends to increase as an asset ages, the specific relationship between age and depreciation is complex. The most straightforward assumption – and often the best assumption, unless one has the data necessary to define a nonlinear depreciation – is to assume a linear relationship. In a linear relationship, asset value declines at a uniform rate across its lifetime until it reaches a residual or salvage value at the end of its useful life.
Where an asset owner has information on the condition of their assets, they can use this information to establish an effective asset age. An asset may last longer than initially expected because it is deteriorating at a lower rate or because it receives treatments to maintain it. In these cases, the asset may have an effective age much lower than its actual age. Conversely, the effective age of an asset may be greater than its actual age, if it is in poor condition, such as that resulting from accelerated deterioration.
One may need to calculate depreciation in a different manner for certain applications. In particular, a more fine-grained calculation of the pattern of consumption of economic benefits may be needed in some cases, particularly if one is calculating initial value considering the stream of future benefits yielded by an asset based on an economic perspective. Chapter 6 presents additional details on the approaches to calculating depreciation, including guidance and examples.
Calculate Value and Supporting Measures
At this point in the process, all of the decisions about how to determine asset value have been made, and only the calculation remains. Every asset valuation requires calculating the initial value for all assets and components, and typically includes some approach to depreciating that value to obtain a current value. Depending on the specific application, this step may also include calculating:
- The cost to maintain asset value;
- Asset Sustainability Ratio (ASR);
- Asset Consumption Ratio (ACR);
- Asset Funding Ratio (AFR);
- NPV for an asset or group of assets; and/or
- Other measures.
Communicate and Apply the Results
Once asset value has been calculated, the final step is to communicate and apply the results. Various approaches have utilized asset value as a communication tool, with several such examples illustrated in Section 2.1. Also in this step, one may need to interpret the results of an analysis to evaluate the significance of any changes in asset value and the values of supporting performance measures.
It is important to document the approach used for calculating asset value, and the key assumptions made in the calculation process. Depending on the specific application, one may wish to perform a sensitivity analysis to establish the impact of changes in key parameter values on the results of an analysis. A sensitivity analysis is useful for describing the accuracy of the asset valuation calculation and highlighting any variables which have a significant impact on the asset value. While sensitivity analyses are always applicable, they are most beneficial in cases where there are numerous assumptions leading up to the final calculation. Many calculation parameters that are presumed to be invariant and known with uncertainty are, in truth, uncertain and prone to vary in the future.
There are different accounting standards in the U.S. and internationally for valuing assets for the purpose of financial reporting. These standards describe best practices in accounting that agencies should carefully consider when valuing assets to support TAM. However, particularly in the U.S., the approach an agency uses to value assets for TAM often differs from that used for financial reporting. The following subsections provide further detail on U.S. standards and international standards, and the applications of these standards to support TAM.
GASB Statement Number 34: Basic Financial Statements – and Management’s Discussion and Analysis – for State and Local Governments published in 1999 (1) describes how U.S. public agencies should prepare their basic financial statements, including the reporting of capital assets. GASB 34 requires agencies to report capital assets by their historic cost, also known as purchase price. This approach is recommended to maintain consistency with the U.S. GAAP.
GASB 34 allows for two different approaches for handling depreciation of capital assets. By default, an asset is depreciated over its estimated useful life. The standard does not specify how depreciation is calculated, only that it should be calculated “…in a systemic and rational manner.” In practice, agencies typically assume an expected useful life by asset class and apply straight-line depreciation.
GASB 34’s alternative approach to account for depreciation is the “modified approach.” In this approach, an asset’s historic cost is reported but no adjustment is made for depreciation. Instead, a separate calculation determines the cost to maintain and preserve the asset at a specific level of service, and this cost is disclosed. The asset is treated as an “ongoing concern”, and the cost of maintaining the asset is considered a part of the cost of operating the transportation system, rather than as an adjustment to the asset value.
The modified approach may be used for infrastructure assets that are part of a network or subsystem of a network. To use the approach an agency must:
- Have an up-to-date asset inventory;
- Perform periodic condition assessments at least every three years and summarize the results;
- Maintain assets “approximately at (or above)” the established condition level based on the three most recent condition assessments; and
- Estimate each year the annual amount to maintain and preserve assets at a specified condition level.
Internationally, the IFRS are the predominant accounting standards. The IFRS Foundation reports that globally 166 jurisdictions and 15 of the 20 G20 countries use its standards (the exceptions are the U.S., Japan, China, India, and Indonesia). As noted in Chapter 1, IFRS standards are not specific to the public sector, and IPSAS standards have been developed for public agency use. However, as a practical matter IPSAS standards typically refer to relevant IFRS standards, so the text here focuses on the relevant IFRS standards.
The IFRS standard IAS 16: Property, Plant and Equipment (2) describes how to calculate costs and depreciation for fixed assets. This standard was developed prior to IFRS Number 13, which is described further below, but it has since been updated to reference it. IAS 16 describes that an organization should recognize an asset at its cost when it is originally acquired. Following the original recognition of the asset, an organization can use one of two models for measuring its value: the cost model or the revaluation model.
The cost model is similar to that described in GASB 34. With this model, the value of an asset is its cost adjusted for depreciation. To calculate depreciation, one must first establish the useful life of the asset considering the expected usage of the asset, expected wear and tear, technical or commercial obsolescence, and legal or other limits on the use of the asset. One must also establish the residual value of the asset once it reaches the end of its useful life and the depreciation method for adjusting its value over time. The standard explains that different depreciation methods may be used and that the selected method should be that which “…most closely reflects the expected pattern of consumption of the future economic benefits embodied in the asset.”
The revaluation model may be used as an alternative to the cost model. In this model, the asset is periodically revalued to determine its fair value. Between revaluations, the cost model is used to adjust the valuation. The standards note that revaluation should be made with sufficient regularity to ensure there is no material difference between the calculated cost and the asset’s fair value.
IFRS Number 13: Fair Value Measurement (3) defines fair value. It recommends using the price of an asset for financial reporting, where this can be determined, and it provides guidance on estimating the price where it cannot. The standard also describes a hierarchy used to categorize fair value estimates based on what type of data are used. Ideally, the fair value is established using Level 1 inputs, the asset’s (or an identical asset’s) quoted price in an active market. When Level 1 inputs are unavailable, Level 2 inputs should be used. These include market prices of similar assets or prices from inactive markets and observable data, such as interest rates. Level 3 inputs, “unobservable inputs for the asset or liability”, are relied on when there is no discernable market, and they are accorded to the lowest priority.
IFRS Number 16: Leases (15) includes additional information relevant to fair value calculations for certain situations. In this standard, fair value is defined in the context of a lessor’s account requirements as “the amount for which an asset could be exchanged, or a liability settled, between knowledgeable, willing parties in an arm’s length transaction.”
It is important to note that while international standards allow for use of either historic costs or fair value for valuing assets, the general trend of public agencies in Europe and Australia has been to value assets based on their depreciated replacement cost (DRC), consistent with the fair value approach. This trend is exemplified by recent U.K. and Australian asset valuation guidance for public agencies (12, 16).
The standards described above are applicable to asset valuation for financial reporting. U.S. agencies must follow GASB 34 for financial reporting, but they are under no obligation to use the GASB 34 asset values for other purposes. Furthermore, they are under no obligation to comply with international accounting standards for any purpose. Nonetheless, the U.S. and international standards are important for defining key concepts and establishing best practices. The different accounting standards have been adapted for use in the context of calculating asset value to support TAM with the following considerations:
- While it is not required, some agencies may prefer to maintain consistency between estimates of asset value prepared for financial report based on GASB 34 and for supporting TAM. The guidance describes an approach for maintaining this consistency where desired.
- Agencies using the GASB 34 modified approach have already made a strong linkage between financial reporting and TAM. This approach requires that an agency uses its asset management systems to calculate the cost to maintain its assets. Given that assets are treated as an “ongoing concern” in this approach, they are not depreciated. Ideally, agencies using this approach should utilize the same cost to maintain assets for TAM and for financial reporting. This helps ensure consistency between the financial asset register and technical asset register (e.g., asset values as captured in an Enterprise Asset Management software system).
- While it is not binding for U.S. agencies, IFRS 13 describes best practices for calculating fair value of an asset. The IFRS concepts, terms and guidance are applicable to U.S. agencies calculating asset value using a cost or market perspective.
Other IFRS and IPSAS standards, as well as the standards and guidance of international agencies based on these, help define concepts, terms, and best practices for aspects of the asset valuation calculation process, such as in establishing useful life, calculating residual value, selecting a depreciation method, and deciding how to componentize assets. These concepts are highly applicable to U.S. agencies calculating asset value for TAM.
Information on asset value and how it is changing may support a number of different applications related to both TAM and financial reporting. When establishing the approach to calculating asset value, it is important to consider which applications the calculation is intended to support. This will then guide subsequent decisions concerning how specifically to calculate asset value.
Section 2.1 discusses a range of different applications of asset value for supporting TAM, and provides examples of approaches for using and communicating asset value. Many of the applications of asset value described in this section are complementary to one another. However, some of the applications require a greater level of detail in the calculation, while others may lead to selecting specific options regarding the nuances of the calculation. For the purpose of this step the different applications can be grouped into the following for the purpose of establishing the primary motivation or driver for calculating asset value:
- Maintaining consistency with financial reporting. In this case, an agency wishes to obtain a calculation of current asset value that is consistent with the agency’s calculation of asset value prepared for its financial reports based on GASB 34 and using historic costs.
- Reporting asset value for TAM. Here the primary motivation for calculating asset value is to report value in a TAMP and/or other documents to be read by the agency’s citizens and oversight groups. In addition to calculating current value, one also typically calculates required maintenance costs, and may calculate other measures. In this case, it is not necessary to maintain consistency with the asset value reported in agency financial reports prepared based on GASB 34, though some agencies may choose to do so.
- Evaluating treatment decisions. In this case the asset value calculation is intended to help evaluate what treatments to perform for an asset, such as when defining an agency’s life cycle policies. For this application, it may be necessary to perform the asset value calculations at a greater level of detail, but once performed the calculations can be used in a TAMP or in support of other applications.
- Determining the benefits to transportation users and society. For certain applications it is necessary to determine the benefits of an asset to users and/or society as a whole – e.g., if determining what assets should have highest priority for resilience investments, or whether an asset merits public investment.
Table 3-1 summarizes these drivers and the implications of each for subsequent decisions regarding how to calculate asset value. For each asset value driver the table lists the value perspective that best supports it. Also, it summarizes the implication of selecting the driver for calculation of asset value, calculation of depreciation and treatment selection.
Table 3-1. Implications of Different Asset Value Drivers on the Calculation Process
| Asset Value Driver | Initial Asset Value (Chapter 4) | Treatment Effects (Chapter 5) | Depreciation (Chapter 6) | Measure Calculation (Chapter 7) |
|---|---|---|---|---|
| Maintaining Financial Reporting Consistency | Calculate value based on historic cost. | Establish cost, useful life and treatment history for construction, reconstruction and replacement. | Depreciate value linearly based on asset age. | Asset Value Asset Consumption Ratio |
| Reporting Asset Value for TAM | Calculate value based on replacement cost or market value. | Establish cost and useful life for construction, reconstruction and replacement. Avoid analysis of historic treatments by using condition data where available. | Depreciate value based on effective age determined using condition data. Use linear depreciation unless a non-linear depreciation pattern has been established. | Asset Value Cost to Maintain Value Asset Consumption Ratio Asset Sustainability Ratio Asset Funding Ratio |
| Evaluating Treatment Decisions | Calculate value based on replacement cost | Establish cost, useful life and treatment effects for all treatments being compared. Avoid analysis of historic treatments by using condition data where available. | Depreciate value based on effective age determined using condition data. Evaluate the benefit consumption pattern in determining how to depreciate. | Asset Value Cost to Maintain Value Net Present Value Asset Consumption Ratio |
| Determining Benefits to Users and Society | Calculate value using an economic perspective. | Establish cost and useful life for construction, reconstruction and replacement. | Calculate costs and benefits expected over the life of the asset in lieu of depreciation. | Net Present Value Benefit/Cost Ratio |
As detailed in the table, it is important to maintain consistency with financial reporting then it is important to adopt a cost perspective and base asset value calculations on historic costs. On the other hand, if one seeks to quantify the benefits of an asset to transportation users and society, then one should adopt the economic perspective.
With the other drivers listed in the table one may adopt a cost or market perspective, and may use different approaches for different asset classes. These two drivers differ from each other in the level of detail they imply. More detail is needed to support making treatment decisions than to calculate an overall value without comparing specific treatment decisions. Thus, in cases where treatment decisions are being evaluated a greater level of detail may be required, specifically with regard to calculating depreciation and treatment effects.
Calculating asset value requires data on the asset inventory, on asset age or condition, and on asset treatments. The availability of asset data, or lack of it, may impact what approach an agency uses for calculating asset value. Also, it may impact what assets are included in the calculation and the level of detail at which calculations are performed.
Collecting and maintaining quality asset data can be a significant investment in and of itself. If needed data are unavailable, an agency may be able to expend additional resources to collect additional data and/or improve data quality. Thus, questions about data availability can become questions about resources: are the resources available to collect the desired data? This section discusses what data are needed for calculating asset value and approaches for assessing asset data.
Table 3-2 summarizes data needs for calculating asset value. This information may be available from a range of agency management systems and data repositories. As indicated in the table, certain types of data are required regardless of the approach one uses. Other data may be needed depending on the specific approach. This point at this step is to determine what data are actually available to help support decisions about the scope of the calculation. Key considerations include:
- Inventory data are critical for the calculation, but the level of detail required in the asset inventory depends upon the specific application. Having a comprehensive inventory of all assets is ideal, but often neither achievable nor necessary for the purpose of calculating asset value. Often it is feasible to use summary data on an asset inventory to calculate asset value – e.g., the distribution of assets by age or condition for a given asset class or subclass. Also, assets are frequently included implicitly as part of another asset rather than being inventoried explicitly.
- Some form of data is needed regarding the current condition of the asset inventory using either asset age, condition, or a mix of the two. This is used to depreciate asset value. Chapter 6 discusses issues regarding calculation of depreciation. Often the availability of this data is a limiting factor in calculating value.
- The availability of treatment data is critical for establishing what treatments are considered in the calculation. This topic is discussed further in Chapter 5. For any treatment that is included it is imperative to have a unit cost. If historic costs are used as the basis for the calculation, then ideally one would have historic costs as well, but historic costs can be approximated given unit treatment costs and information on asset age.
- Various other parameters may be required for the asset value calculation, particularly if calculating market or economic value. These approaches are discussed further in Chapter 4.
Table 3-2. Data Needs for Asset Value Calculation
| Inventory Data | |
| Always Needed Asset quantity by:
| May Be Needed
|
Challenges
|
|
| Condition Data | |
Always Needed
| May Be Needed
|
| Treatment Data | |
Always Needed
| May Be Needed Historic data on treatments performed by:
|
Challenges
|
|
| Other Data and Parameters | |
Always Needed
| May Be Neeeded
|
Challenges
|
|
In assessing what data are available, one should also consider the quality and completeness of the data, noting any significant concerns. Common issues in this regard include, but are not limited to:
- Data may be available for a given subset of the inventory (e.g., for a given asset class and/or district), but may not be available consistently across the agency. For many asset classes data on a statistical sample of the assets are acceptable.
- Inventory and/or condition data may be available for a given point in time, but may not be consistently maintained.
- There may be limited data on what treatments have been performed on a given asset since it was first constructed. This can be an issue if one is relying on asset age rather than condition to establish depreciation, particularly if one also seeks to include other treatments besides asset construction/reconstruction in the approach.
- There may be other changes over time that changes in data over time that may difficult to track and that further complicate use of historic data. This may include changes in the network (e.g., which highways are included in the NHS), changes in asset ownership, and/or changes in data collection approaches.
- Information on current and predicted future asset use needed for calculating economic value may be unavailable or difficult to obtain.
The process of assessing the data available for calculating asset value may be performed as part of a broader assessment of an agency’s asset data resources and needs. NCHRP Report 956: Guidebook for Data and Information Systems for Transportation Asset Management presents an approach for assessing an organization’s current data and information management practices in support of TAM, as well as strategies for improving these practices (17). An agency can apply the guidebook comprehensively to all of the organization’s TAM activities or use it to focus on particular components, such as components related to calculating asset value.
Figure 3-1 reproduces the “Data Life-Cycle Framework” from NCHRP Report 956. This shows the different elements of an organization’s asset data included as part of an assessment. The framework organizes the assessment items into five categories. Of these, two are most relevant for assessment of data for asset valuation: A. Specify and Standardize; and B. Collect.
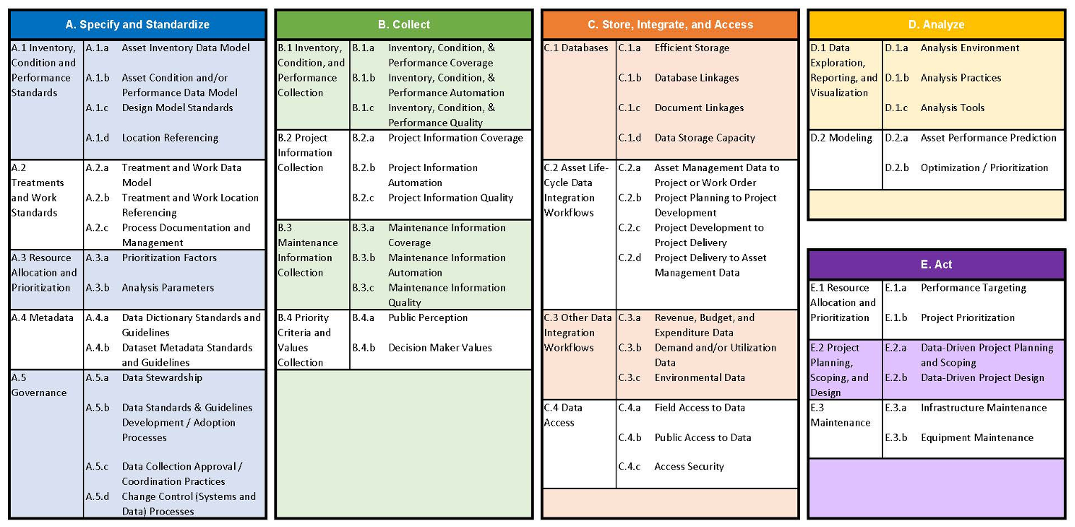
NCHRP Report 956 is accompanied by a web tool, the TAM Data Assistant, to support the assessment of TAM data needs. Together the guidebook and the tool offer an organized process for evaluating and improving an agency’s data systems. This web tool is hosted by AASHTO and available for public agency use.
The screenshots below show the primary two steps in the tool’s process. First, users assess their data system using benchmarks provided for each of the five areas outlined in Figure 3-1. Then, in the screen on the right, they evaluate their selected improvements to prepare an implementation plan.

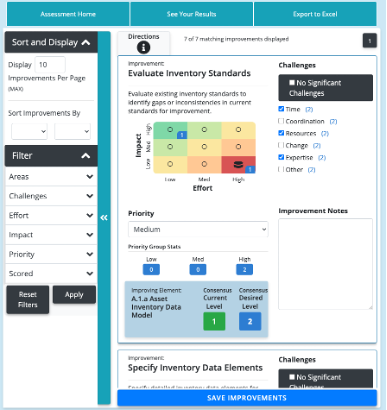
In addition to guidance for the TAM Data Assistant, the report provides case studies demonstrating the importance and impact of data improvements across state DOTs and resources for those facilitating the assessment. For more information about the tool and the NCHRP Report, visit www.tamdataguide.com.
Source: NCHRP Report 956 (17)
After establishing the motivation for calculating asset value and reviewing available data, the next step is to identify which assets will be included in the valuation calculation through establishing an asset hierarchy. An asset hierarchy is a framework for organizing a set of assets. It specifies asset classes and sub-classes, as well as any parent-child relationships between different types of assets.
Note that an organization may already have established an asset hierarchy that can be used to support this step. Alternatively, one may establish a hierarchy specifically for the purpose of calculating asset value. In any case, it is important to note that the set of assets included in the asset value calculation may be different from that defined for other purposes. Thus, if one is referencing an existing hierarchy, it will be necessary to further note which assets are included explicitly in the asset value calculation, which are included implicitly as part of some other asset, and which are excluded.
Assets exist within a network, and they rely upon the collective maintenance of the network to function properly. If some assets in these networks are not explicitly valued, their impact should be accounted for implicitly within the valuation. Also, at this point practitioners should establish whether the asset value calculation is focused on specific systems or subsets of assets. Asset subsets comprise its inclusion within a system (e.g., on the NHS or Interstate), ownership of the asset (federal, state, or local), and the asset’s geography.
A final consideration for the asset hierarchy is ensuring that assets excluded from the analysis are not neglected in maintenance or other investments. By analyzing assets within a network or along a corridor, one can weigh all aspects of maintenance for all levels of assets, from geotechnical structures to the pavement markings.
The following subsections describes common classes of transportation assets and considerations in calculating asset value for each.
Minnesota DOT (MnDOT) includes calculates value for pavement and bridge assets in its 2019 TAMP, as well as for culverts, tunnels, signs, light towers, noise walls, signals & lighting, pedestrian infrastructure, buildings and ITS. The table displays MnDOT’s full asset hierarchy.
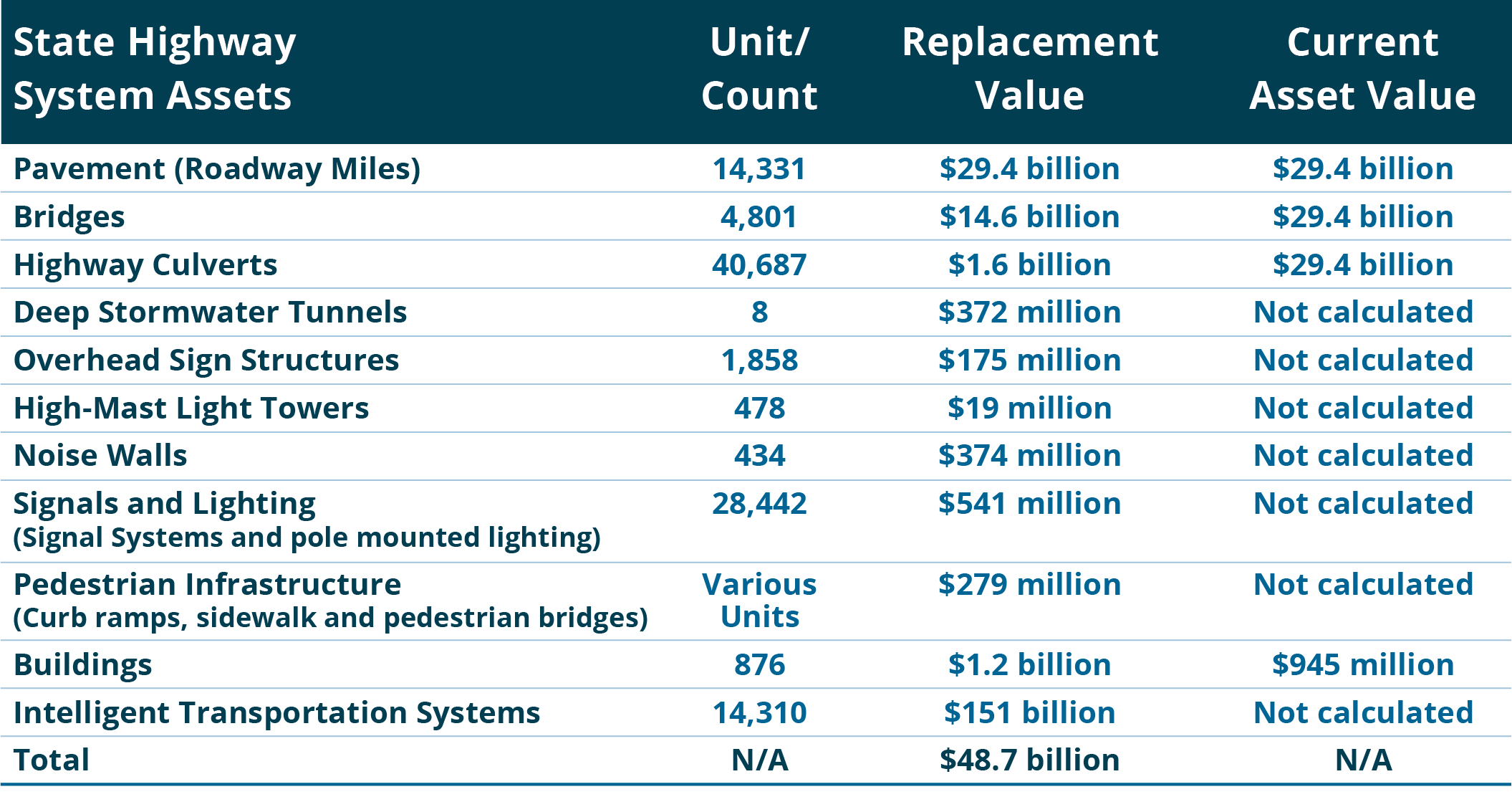
Source: Minnesota DOT (29)

This asset includes the wearing surface of roads, runways, sidewalks and other paved surfaces, as well as the other layers supporting the wearing surface. For highway agencies pavement is typically the asset with the greatest overall value; it is the asset a highway department has the most of. State DOTs are required to estimate the value of their NHS pavement in their TAMPs.
State DOTs are required to maintain an inventory of their roadway pavement through the Highway Performance Monitoring System (HPMS), and to collect condition data for different pavement distresses for pavement on the NHS. A challenge in managing pavement data is that pavement is a linear asset, and can be sectioned in different ways. For instance, condition data may be collected and reported for 1/10-mile sections, while longer management sections are used for predicting future conditions and developing projects.
Frequently, asset value calculations include a number of additional assets as part of the valuation of pavement, to the extent these additional assets may be replaced or reconstructed as part of a project to replace or rehabilitate the pavement. This may include shoulders, curbs, pavement markers/markings, signs, and drainage assets. Also, sidewalks and bike paths, though paved, are often treated as separate assets from roadway pavement.
Pavement life varies by material type (e.g., asphalt, concrete, hybrid, etc.), operating environment, how the pavement is maintained, how the end-of-life is defined, and what specific assets are included as part of the pavement asset. Typically, the wearing surface of a road is assumed to last approximately 20 years, while the “full-depth life” which includes multiple rehabilitation treatments of the wearing surface, is assumed to be approximately 50 years (18).

This asset class includes constructed works that allow a road to span a physical obstacle, such as a river or other road. For a highway agency structures are typically the asset class with the second greatest value following pavements.
Here this asset class is defined to include bridges and tunnels, and culverts. In practice the terms “structures” and “bridges” are often used interchangeably. In the U.S. bridges, tunnels and larger culverts are all included in the National Bridge Inventory (NBI) and State DOTs are required to estimate the value of their NHS structures in their TAMPs.
State DOTs are required to maintain an inventory of all bridges on public roads in their state. Also, State DOTs are to report condition data for the bridges in the state, collected through periodic visual inspections.
Structures are long-lived assets. As a practical matter, a structure can remain functional for 100 years or more if it is appropriately maintained. However, structures are often replaced when replacement is the most cost-effective alternative for addressing deterioration, or if the structure has functional issues that render it obsolete (e.g., designed for smaller loads or traffic levels than current standards). Based on review of the 2019 State DOT TAMPs, DOTs typically assume a design life of 75 years for their structures for the purpose of calculating asset value.

This class includes a number of different assets that either enhance mobility and/or improve safety. This includes, but is not limited to:
- Signs and their supporting structures
- Traffic signals
- Lighting
- Guardrail, median barriers, cable barriers and other impact attenuators
- Pavement markings and markers
- Intelligent Transportation Systems (ITS) devices such as cameras, other sensors and detectors, and variable message signs
- Tolling systems
- Grade crossings
Practices regarding management of traffic and safety assets vary widely between specific asset types and agencies. NCHRP Synthesis 371 provides a summary of current practices and typical asset lives for several common types of assets (19). Service lives for traffic and safety assets range from one to two years for certain types of pavement markings to 20 years or more for guardrails and median barriers.
Generally, agencies lack data on asset condition for many traffic and safety assets, as collecting condition data can be impractical and condition is often a poor predictor of when the asset needs to be replaced. Furthermore, many agencies have limited or incomplete inventory data on these assets, which is the starting block for collecting condition data. In many cases, traffic and safety assets are replaced due to functional obsolescence rather than as a result of their physical deterioration. As noted above, these assets are frequently replaced as part of a larger effort to rehabilitate a section of pavement or a corridor, and thus, they are often valued as part of the pavement asset class.

Vehicle assets include revenue and maintenance vehicles, such as buses, paratransit vehicles, ferries, train cars, tow trucks, plows, and various other types of service vehicles. For State DOTs vehicles are often a small portion of an agency’s inventory. On the other hand, for transit agencies revenue vehicles typically represent the largest single asset class an agency owns based on asset value.
The Federal Transit Administration (FTA) has published assumed useful lives, termed “useful life benchmarks,” for a range of vehicle types (20). Default values are 8 years for four-tired vehicles such as automobiles and vans, 14 years for buses, 31 years for light and heavy rail vehicles, and 39 years for commuter rail coaches and locomotives.
Agencies track inventory data on their vehicles, but approaches vary regarding tracking condition data. Often age or vehicle mileage is used as a proxy for asset condition. Transit agencies report data by vehicle subfleet for revenue and service vehicles to the National Transit Database (NTD).
A notable feature of vehicles is that relative to fixed assets they are more easily transferred from one owner to another. Thus, it is often feasible to establish a market value for vehicles using information on the sale or auction of used vehicles.

For transit systems that operate light rail, heavy rail or commuter rail, fixed guideway is a significant asset class. This includes track, communications and signals, and electrification systems. For the purpose of reporting to the NTD, transit agencies group other fixed assets besides facilities into the category of “Infrastructure.” In the NTD this category also includes structures and guideway for bus rapid transit systems that are addressed above in structures and pavement.
It is difficult to generalize management approaches and asset lives as these vary significantly between different asset subclasses and agencies. Generally fixed guideway assets tend to be long-lived. Track requires periodic rehabilitation but can be maintained indefinitely. Communications, signals, and electrification assets have varying lives which are often dictated by consideration of functional obsolescence rather than physical condition. Transit agencies report data on their inventory and its age to the NTD. FTA describes different guideway assets and management approaches in its Transit Asset Management Guide (21).
Transportation agencies own and operate a number of facilities. Typical facilities for highway agencies are discussed in (22) and include:
- Administrative facilities
- Maintenance depots;
- Rest areas;
- Toll plazas;
- Weight stations; and
- Communications facilities.
Transit facilities are classified in the NTD as either: administrative/maintenance facilities such as office buildings, bus garages or rail yards; or passenger facilities such as stations and parking garages. Airport facilities include many of these same types, as well as aircraft hangars, terminals, fueling facilities and baggage handling facilities. Many facilities include major pieces of equipment (e.g., vehicle lifts) that may be inventoried separately or considered as part of the facility.
Like structures, facilities are typically complex, with many different components, and have a seemingly indefinite lifespan. Overall facilities lives are estimated as 50 to 100 years in models such as FTA’s Transit Economic Requirements Model (TERM) Lite (23). Similar to vehicles, in some cases facilities may be transferable to other owners, simplifying the calculation of a market value for a facility.
Transportation agencies manage various other assets not addressed in the classes discussed above, including:
- Drainage: this encompasses pipes, gutters, drains, retention/detention ponds, and others. Management of drainage assets is complicated by the fact that many are underground and difficult to inventory. Also, in many cases it may be difficult to establish maintenance responsibility for drainage assets.
- Geotechnical: NCHRP identifies four basic subclasses of constructed geotechnical assets (24). These are slopes, embankments, subgrade, and retaining walls. Agencies may also identify geohazard locations (e.g., potential rockfall locations) in an asset inventory. As in the case of drainage assets, it can be a challenge to establish an inventory of geotechnical assets. Typically, these assets are long-lived, with asset lives similar to structures.
- Bicycle and Pedestrian Assets: bike lanes, sidewalks, curb ramps, and other related features. These assets promote multimodal accessibility, and in some cases (e.g., curb ramps) may be needed to comply with the legal requirements such as the Americans with Disabilities Act (ADA). Typically these assets have lives similar to traffic and safety assets described above.
- Land: this includes right-of-way, land used for facilities, and other land owned by a transportation agency. Land is different from other transportation assets regarding calculation of asset value in that it is not assumed to depreciate. Also, methods established for calculating the market value of real estate are directly applicable for valuing land, with the additional complication that in many cases there is additional value associated with maintaining a corridor (e.g., for construction of a future transportation link or fiber optic cable). Transportation agencies typically do not calculate a value for their land for TAM applications given it does not vary as a function of TAM-related decisions. However, land value can be highly relevant for decisions where the privatization of assets is evaluated, or where the overall benefit of an asset to society is considered.
In the context of this document, componentization is defined as the process of delineating parts of an asset – components – for which the asset value calculation is performed separately. Defining asset components may be necessary to obtain an accurate calculation of asset value, depending on the nature of the assets being valued and the intended application of the asset value calculation. The following subsections discuss the reasons for defining asset components when calculating asset value, specific criteria for when to componentize, and asset classes where componentization may be considered.
The basic reason one may wish to break an asset into components is that it may be a complex asset with different elements that have different asset lives. If the only treatment one performs on an asset is to replace it then this detail is immaterial. In this case the remaining life of an asset is dictated by the minimum remaining life of the different components of the asset. However, if it is feasible to treat individual components of an asset, extending their life while leaving the life of other portions of the asset unchanged, then the situation is more complex. In this case, considering the different asset components yields a different and arguably more accurate calculation of value than performing the calculation only for the asset as a whole.
An asset that is commonly decomposed into components is a bridge, as discussed further below. Figure 3-2 shows how a bridge may be valued over time with and without calculations at the component level. The upper panel shows the asset value of the bridge by year, subdivided by components (deck, superstructure and substructure). The components have different asset lives and thus depreciate at different rates. At three points in time the value is increased as a result of a treatment performed on a component (the deck and/or superstructure).
The lower panel shows the value if calculated at the bridge level. In this case the value declines more gradually over time, and the treatments applied at a component level do not impact the overall value. Asset value at the beginning and end of the analysis is the same in both cases. However, the component-level representation more accurately reflects the effects of different treatments.
Note that in this case, various complicating factors have been omitted. Most notably, in this case, depreciation is based on component age. In reality for asset management applications, it is common to base depreciation on condition where condition are available.
Based on the above discussion, the following criteria are recommended for establishing when to perform the asset value calculation at the component level. Specifically, componentization is recommended in cases where:
- The asset represents a significant portion of the value being calculated;
- The asset is complex, with different identifiable components aging at different rates;
- Multiple treatments are performed to the asset over its life extending the life of different components;
- Data are available on the inventory of asset components and on either their condition or age to support calculation of depreciation; and
- The driver for calculating asset value is to evaluate different treatment options, or there is significant interest in doing so.
Agencies may establish additional criteria for when to value assets at a component level. The example below describes guidance for valuing assets at a component level. For example, Austroads describes that an asset over $5 million should be componentized when the asset structure can be separately identified, the different parts can each be measured, and the components have different service lives (24). The example below illustrates the componentization approach recommended by CIPFA for local agencies in the U.K.
The Chartered Institute of Public Finance and Accountancy (CIPFA) has established an asset hierarchy and componentization approach for the purpose of calculating asset value to be used by local agencies in the U.K. (16). In its guidance CIPFA defines three levels in the hierarchy:
- Level 1: Component Type – broad categories based on the general function of the components. They divide the Highways Network Asset into categories of components and provide an appropriate basis for high-level management information.
- Level 2: Component groups – used to distinguish between component types that have a similar function and form.
- Level 3: Elements – distinguishes between components that, at least when systems become well developed, may require individual depreciation and impairment models, such as different service lives and/or rates of deterioration.
The table depicts how these levels are defined for pavement (carriageways).
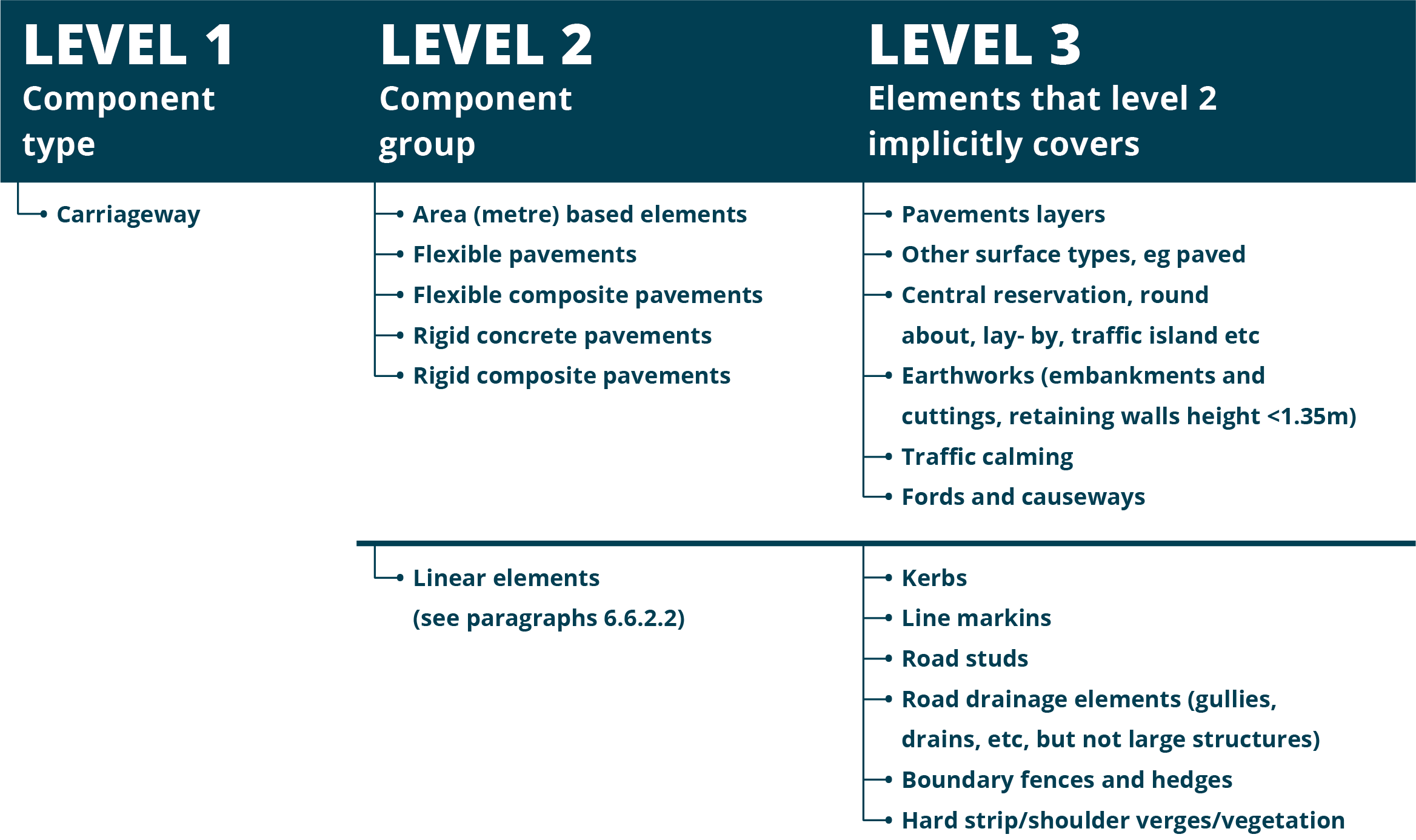
Source: CIPFA (16)
The transportation asset classes that are most commonly divided into components are pavement and structures. Other asset classes that may be componentized are facilities and fixed guideway. Below are specific considerations regarding these asset classes.
Pavement
Pavement may be split into components, but doing so is the exception rather than the rule in U.S. practice. Where pavement is componentized, typical components include the pavement surface, base, subbase, and subsurface, as illustrated in Figure 3-3. This approach is used by agencies such as New Hampshire DOT TAMP (25), and recommended in by Austroads (26).
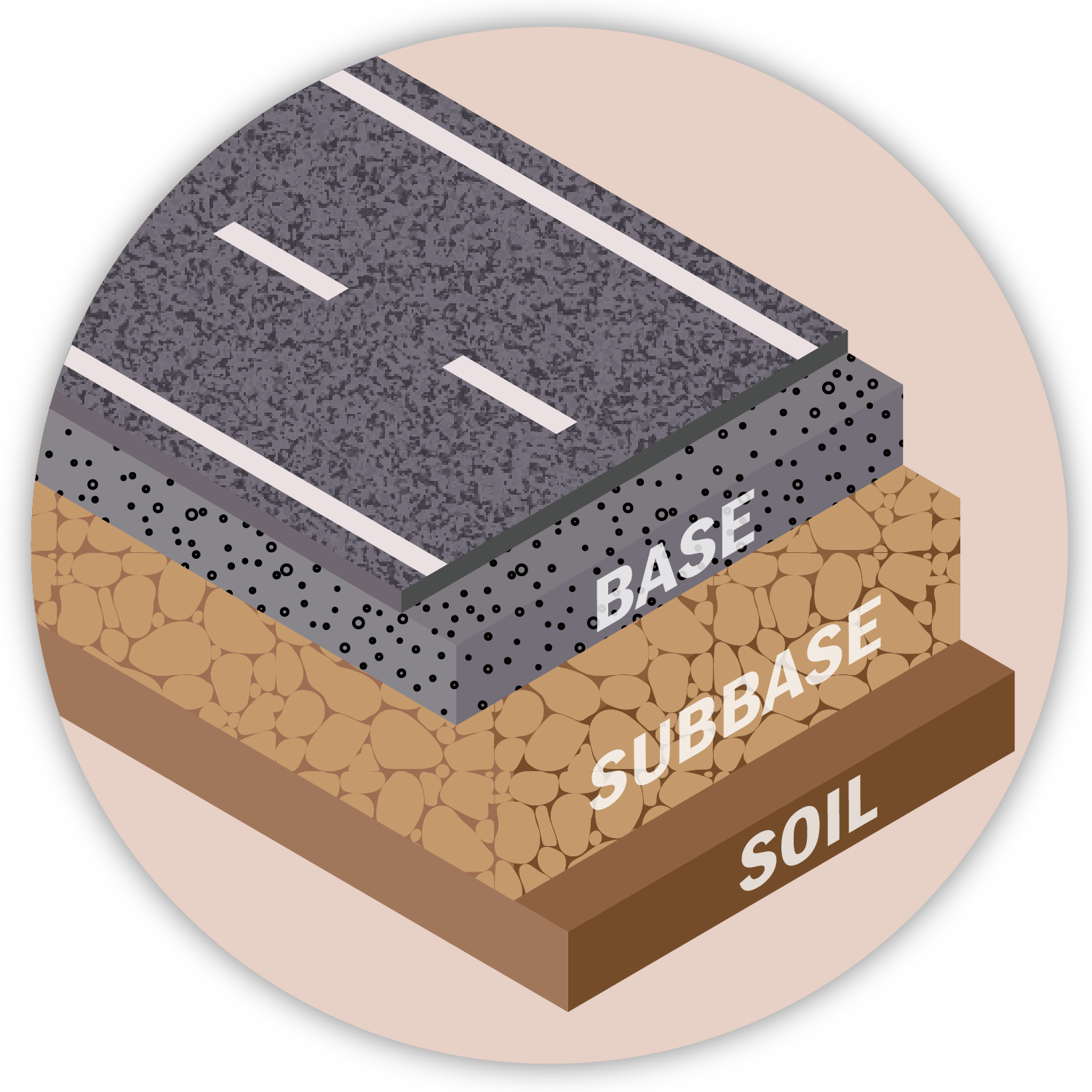
The challenge in valuing individual pavement components is that most condition data collected for pavement, such as roughness, rutting, cracking and faulting, are measures of surface distresses. Limited data are available regarding the underlying condition of the pavement structure and base, though increased surface distress may result from deterioration of the pavement structure. A further consideration is that while it is possible to treat the pavement surface without treating the pavement structure, the converse is not true: any treatment that impacts the structure or base of the pavement also effect the surface.
The basic approach that one can use to address the complexity of pavement without breaking it into components is to calculate an effective age for a pavement section that adjusts the actual age of the pavement (which captures the age of the base and structure) using condition data (which best represents the surface of the pavement). Also, agencies typically introduce business rules in developing their lifecycle strategies to limit the number of times that an overlay or other surface treatment can be performed without more extensive rehabilitation of the pavement structure.
Structures
Structures – particularly bridges and tunnels – are complex assets that typically meet the criteria provided above for componentization. Where bridges are componentized, the typical components are the bridge deck, superstructure and substructure as depicted in Figure 3-4. The NBI includes visual ratings of these components, simplifying the task of componentizing for U.S. highway bridges. To support a componentized approach, one must determine what portion of the asset value is comprised by each component, and then value each component separately. Chapter 8 provides an example of a component-level calculation of asset value for structures.
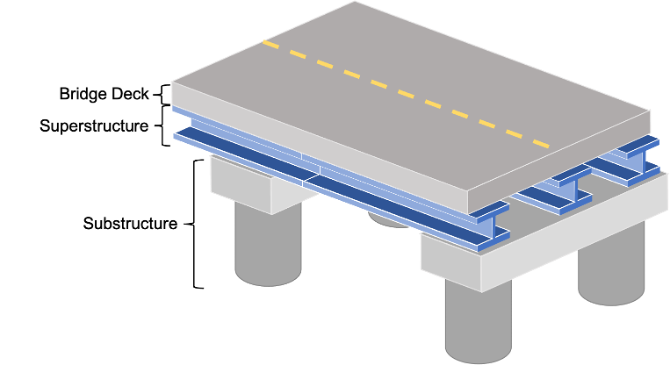
For all NHS bridges and many other state-owned bridges, state DOTs also collect more detailed condition data for structural elements based on AASHTO specifications. This data provides the basis for componentizing at an even greater level of detail if desired. Figure 3-5 shows an example of the structural elements of a bridge.
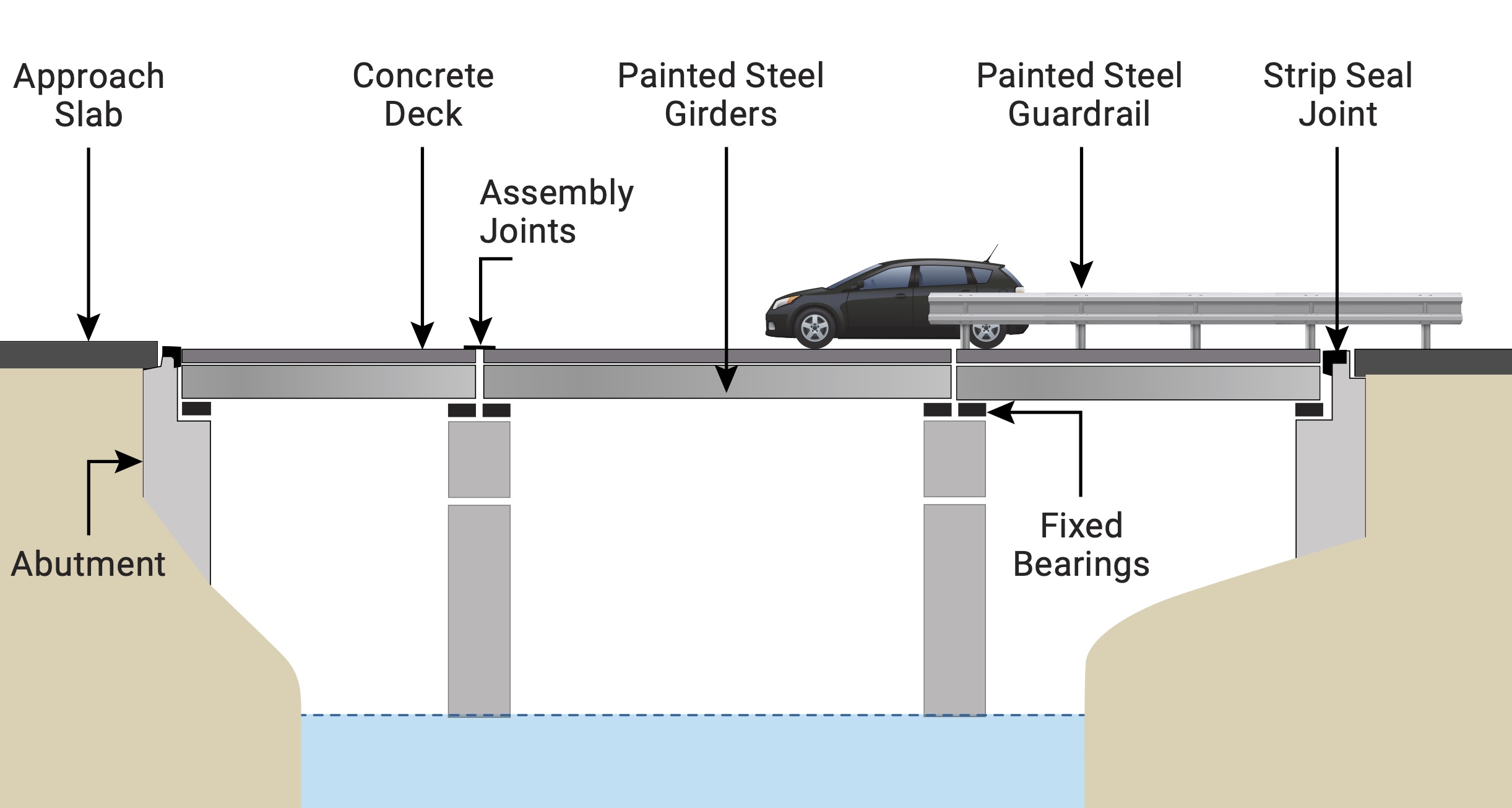
Tunnels are extremely complicated structures and should be valued using a componentized approach where feasible. Components of highway tunnels are defined by FHWA in the Specifications for the National Tunnel Inventory (27). These include: structural elements (similar to bridges); civil elements (e.g., barriers and railings), mechanical systems (e.g., ventilation and drainage); electrical and lighting systems; and fire and life safety systems.
Other Assets
Facilities and fixed guideways are examples of asset classes that may be componentized, depending on data availability and the specific application of the asset value calculation. There are no widely accepted standards for assessing or componentizing highway facilities in the U.S. Regarding transit facilities, FTA has developed guidance for inspection of facility systems, subsystems, and components such as the substructure, shell, interiors, plumbing and electrical systems (28). Transit agencies assess conditions of their facilities and report their overall condition to the NTD. Fixed guideway is a complex asset and ideally should be componentized (e.g., into track, communication, and electrification subclasses). However, there are no specific standards in the U.S. for how to componentize and assess different guideway assets.
Initial asset value is the value of an asset at the start of the analysis period. What this represents, exactly, depends on the approach being used to make the calculation. In some cases, the initial value is the value of an asset when first constructed or acquired, while in others, it may be the value at a particular point in time.
This guide describes four basic approaches to calculating initial value. These are as follows:
- Current Replacement Cost – the cost of replacing the asset with its modern equivalent in today’s dollars. This is also referred to as the “gross replacement cost. When this approach is used, the initial value is the cost of constructing or acquiring a new asset. The cost is then adjusted for depreciation to obtain a “depreciated replacement cost” a described further in subsequent chapters. This approach is consistent with the cost perspective described in Section 2.
- Historic Cost – the actual cost paid to first construct or acquire the asset, expressed in year of expenditure dollars. When this approach is used, the initial value is the historic cost constructing or acquiring the asset. This approach is consistent with the cost perspective described in Section 2.
- Market Value – the price of an asset if offered for sale in a competitive market. This value can be established only if such a market exists. In this approach, the initial value is the price of an asset at a specific point in time. Further adjustment to this price may be required to account for recent appreciation or depreciation. This approach is consistent with the market perspective described in Section 2.
- Economic Value – the present value of the benefits of an asset to the asset’s owner, and asset users. When this approach is used, the initial value is the sum of future benefits of the asset at a specific point in time. Costs and benefits over time are discounted to a present value when they are combined. This approach is consistent with the economic perspective described in Section 2.
Table 4-1 summarizes the strengths and weaknesses of each approach.
Table 4-1. Approaches for Establishing Initial Value
| Approach | Description | Strengths | Weaknesses |
|---|---|---|---|
| Current Replacement Cost | Cost of replacing or reconstructing the asset in today’s dollars |
|
|
| Historic Cost | Cost originally paid to construct or purchase the asset |
|
|
| Market Value | Price of the asset in a competitive market |
|
|
| Economic Value | Present worth of future benefits to asset users (or a comparable proxy value) |
|
|
Replacement Cost
The replacement cost of an asset in today’s dollars represents the value of an asset from the perspective of the asset manager charged with deciding which assets to repair, rehabilitate, or replace using today’s dollars. Not surprisingly, many U.S. agencies base their estimate of asset value on asset replacement cost in their initial TAMP, and much of the U.S. and international guidance on calculating asset value to support TAM describes this approach.
Historic Cost
This approach differs from the replacement cost approach in its treatment of inflation. When using historic cost, one obtains the actual cost incurred to purchase or construct the asset in the year-of-expenditure dollars. This value is almost always less than the current replacement cost, or the cost of replacing the asset in today’s dollars, because the current replacement cost reflects the inflation that has occurred since the asset’s construction.
The historic cost is consistent with the U.S. GAAP and U.S. agencies’ calculations of asset value for financial reporting. However, historic costs have limited use for supporting decisions about how to spend today’s dollars. Further, it is frequently difficult to obtain historic cost data for individual assets or asset components, especially for older assets.
Market Value
Where a market exists for an asset, using the market value can simplify the process of calculating both initial value and depreciation, because both aspects are reflected in the market price. A market price also encapsulates the cost of the asset from the owner’s perspective and the economic benefits of the asset from the user’s perspective, helping to integrate the different perspectives concerning what asset value represents. Using the market price to establish fair value is consistent with the international accounting standard IFRS 13.
Economic Value
The economic value can be calculated explicitly as the net present value (NPV) of future benefits or approximated via a utility function that represents these benefits. Calculating the economic value of an asset is consistent with the concepts of benefit-cost analysis and offers the best support for certain types of decisions, like determining which assets to prioritize for resilience investment, retention, or new construction. However, this is the most time-consuming and data-intensive approach of the four listed here. For supporting day-to-day decisions regarding how to maintain existing assets, the additional information the economic value yields may be of limited use.
Figure 4-1 is a flowchart to assist in the selection of an approach for calculating initial asset value. The chart recommends current replacement cost as the default approach for establishing initial asset value, while presenting the cases where one of the other approaches may be preferred. The basic factors and assumptions reflected in the flowchart are as follows:
- Historic cost is not recommended for establishing initial value but should be used in cases where an agency seeks to maintain consistency with its calculation of asset value performed for financial reporting using GASB 34.
- Economic value is recommended for certain, specific applications, such as when the asset manager seeks to calculate the overall value of the asset to society in order to establish if an asset is worth constructing or decommissioning. For these cases, simply knowing the cost of an asset is insufficient for determining whether it is worthy of investment.
- In the situations where the market value of the asset is available, it should be used over the current replacement cost. When market value is not available, current replacement cost should be used.
This section describes how to calculate initial asset value using each of the four methods described previously: current replacement cost; historic cost; market value; and economic value. The following subsections discuss issues specific to each approach and provide step-by-step guidance. This guidance should be applied for calculating value for each asset class and component identified previously as described in Chapter 3. Since economic value differs significantly from the other three approaches and is recommended only for specific applications, details of this approach are provided in Appendix 4.A.
Overview
Calculating the current replacement cost of an asset may seem to be a straightforward exercise, and generally speaking it is. One must establish a unit cost for construction of a new asset, determine the quantity of the asset, and multiply the cost by the quantity. However, at each step of the way there are possible complications that one must consider. These include:
- Determining the units of measure for an asset. This requires considering what factors drive the cost. For instance, for pavements and bridges costs are generally proportional to area (lane miles of pavement or square feet of deck). For other assets costs may be expected to vary based on system length or other variables.
- Establishing the number of different asset groups. That is, how many different unit costs need to be determined? At a minimum, there should be at least one unit cost per asset component established as described in Chapter 3. In many cases, there may be different costs established by material (steel versus concrete bridges) or functional system (Interstates versus minor arterials).
- Adjusting historic data for inflation. Often an analysis is performed of actual, historic costs to determine the current replacement cost. Where such an analysis is performed historic costs must be inflated to today’s dollars.
- Deciding when an asset would need to be replaced by its modern equivalent. In some cases, it may not be practical or desirable to replace an asset in kind, such as in cases where an asset is based on obsolete technology. It is important to consider where this might be the case, and in these cases establish the cost of replacing an asset with its modern equivalent.
While it is possible to calculate a specific cost for each individual asset in an inventory, as a practical matter, agencies’ asset inventories are often too large to justify the expense of preparing detailed cost estimates for each individual asset. To support TAM applications, agencies need to establish unit costs to use for estimating the cost of asset replacement.
Calculation Steps
The basic steps involved in calculating current replacement cost using unit costs are shown in the following table. These steps should be followed for each asset class and component being included in the calculations.
- Step 1 – Determine Units of Measure:
Analyze the data to determine the correct units of measure to use for each asset class and component for the purpose of estimating replacement costs. Typically, costs are estimated based on area (e.g., for pavement and bridges), length (e.g., for guideway) or asset count (e.g., for vehicles).
- Step 2 – Collect Data on Replacement Costs:
Collect data on the cost of replacing each asset class and component defined as described in Chapter 3. The data may include historic asset construction costs and/or cost estimates for planned projects, as well as data on units of measure established in Step 1. Where data are unavailable, it may be possible to obtain data from an agency’s peers.
- Step 3 – Adjust Costs for Inflation:
Adjust the costs obtained in Step 1 to represent costs in today’s dollars. This will typically require inflating historic costs and may require deflating any predicted future costs. Appendix 4.B discusses the treatment of inflation.
- Step 4 – Determine How to Group Assets:
As necessary, create different groups for asset classes or components to reflect differences in replacement costs. Asset characteristics such as roadway classification, rural or urban setting, regional factors, and asset materials may impact replacement costs.
- Step 5 – Calculate Unit Costs for Each Group:
Using the data for each asset group, take the sum of the construction costs and divide by the total area, length, or count (depending on the asset type).
- Step 6 – Apply Unit Costs:
The last step is to multiply the unit costs established in Step 5 by the quantity of each asset or asset component to determine the current replacement cost.
Overview
The primary motivation for establishing initial value based on historic cost is to maintain consistency with an agency’s financial reporting. Requirements for U.S. agencies to use for preparing financial reports are described in GASB Statement 34 (1). This document describes that:
Capital assets should be reported at historical cost. The cost of a capital asset should include capitalized interest and ancillary charges necessary to place the asset into its intended location and condition for use. Ancillary charges include costs that are directly attributable to asset acquisition—such as freight and transportation charges, site preparation costs, and professional fees…
In principle, determining the historic cost of an asset should require nothing more or less than reviewing an agency’s financial records to determine the cost paid to first construct or acquire the asset. Where sufficient data are available to support this approach, one should determine the cost of construction or acquisition, as well of capitalized interest and ancillary charges as described above.
The fundamental challenge with this approach is that records on historic costs may not be readily available, and where they are available may not provide a sufficient level of detail for establishing the cost by asset class or component. For instance, one might have a single cost from the time a highway corridor was first constructed – but without details on the amount paid per section of pavement or per bridge, let alone for assets such as signs, signals, culverts, guardrails and other assets – some of which may have been completely replaced since the corridor was constructed. The challenge is compounded by the fact that many transportation assets are long-lived, so one may need to review extensive historic data to establish the costs for a given asset.
Many agencies have faced this challenge in calculating historic costs since GASB Statement 34 was first published in 1999. A basic strategy for overcoming it is to estimate replacement costs by asset class using unit costs expressed in today’s dollars, then deflate the estimated cost back to year-of-expenditure dollars using information on asset age. This approach is termed the “Wooster Method” as its use was first documented in a financial report for the Town of Wooster, Ohio (6).
Calculation Steps
The following are the basic steps involved calculating initial asset value using historic costs with this approach:
- Step 1 – Collect Data on Asset Age:
Collect data on asset age for the assets and asset components established as described in Chapter 3. If the age of specific assets is unavailable, then the age distribution of the inventory may be used as an alternative.
- Step 2 – Calculate Current Replacement Cost:
Follow the steps in the previous section to calculate current replacement cost for each asset class and component.
- Step 3 – Deflate the Current Replacement Cost:
Deflate the current replacement cost based on the asset age data collected in Step 1 to obtain estimated historic costs. Appendix 4.B discusses the treatment of inflation.
Overview
Where a competitive market exists for an asset, it may be feasible to establish the asset’s market value. This market value represents the current value of the asset. Unlike the current replacement cost and historic cost approaches, this value incorporates accumulated depreciation since the asset was first constructed or acquired.
Because many transportation assets are fixed in place, it is the exception rather than the rule that a market value may be determined. In most cases it is not terribly practical to transfer a transportation asset from one owner to another. There are two primary exceptions to this rule. One is the case of vehicles and equipment that can be easily transferred, and the second is the case where a market value is established for the purpose of privatizing infrastructure, such as to issue a concession to a private entity to operate and maintain a toll road. These two cases are described below.
Vehicles and Equipment
In many cases it is possible to perform an independent fair market value assessment for vehicles and equipment, as these assets are readily transferrable from one owner to another. Where a market value can be established, this value indicates what the market is willing and able to pay for a specific vehicle or piece of equipment, taking into consideration prior use, current condition, remaining useful life, and other factors. In some cases, a vehicle or piece of equipment may have significant remaining value even once it is replaced by an agency. However, older or damaged assets may have a remaining value equal to their scrap or disposal value.
Used vehicle fleets are often valued and sold via a broker, auction houses, or other third-party tools. In some cases, fleets are sold to other agencies. Where such an approach is used, a market value is determined for the fleet, which can be equated to a value per vehicle.
For non-revenue vehicles and pieces of equipment, it is more common for any transactions to occur through private party transactions or auctions. In these cases, an independent fair market value assessment of the asset is often performed, such as through referencing guides such as the Kelley Blue Book for used vehicles (30), and other industry guides.
Privatized Infrastructure
When evaluating opportunities for privatizing transportation infrastructure, investors typically classify the different opportunities as either “green field” or “brown field” investments. In this context, a “green field” investment is one in which a new facility is constructed where none previously existed – e.g., a new toll road or transit system. By contrast, a “brown field” investment is one where an asset that is already operational is transferred to private control in exchange for some price. Such “brown field” investments, where they occur or are evaluated, provide an opportunity for establishing the market value of transportation assets.
Investors evaluating a brown field investment consider a variety of different risks and factors, also termed “key value drivers.” Once they have identified these drivers, investors will perform forecasts and financial analyses on the key value drivers to determine the market value of a given investment.
Below is an example of the key value drivers for a toll road concession.
- Asset Type: different toll road asset types present a different set of risks to an investor that is valuing a brown field toll road. For instance, a highway system or large network of toll roads that connects major population centers may have more diversified traffic types, routes, and asset maturity. As a result, they are often resilient to fluctuations in economic conditions. By contrast, a standalone road in a rural area may be more speculative in terms of revenue generation. Brown field asset valuations benefit from a demonstrated history of traffic that allow an investor to compare the actual level of traffic vs. original forecasts.
- Remaining Concession Term: in a toll road concession structure, investors will consider the remaining term of the concession with a public sponsor, as the term length is a significant driver of the length of time that an investor can generate cash flow. Term of the concession refers to the length of a contract between a developer and a public sponsor to design, build, finance, operate, and maintain a toll asset (usually anywhere from 30 to 99 years). In a brown field valuation, the asset has already been designed, built, and originally financed. When an original concessionaire sells its stake in a toll road, the concession term typically remains static. Thus, the ability to generate cash over the remaining concession term will directly impact the price that an investor is willing to pay for an asset. In general, the longer the concession term, the higher the price that an investor would be willing to pay for the asset, as the investor has a longer period of time available to generate a return on investment. Further, longer concession terms may provide opportunities for investors to issue additional debt to further leverage the asset, which will ultimately increase the asset’s value. The economic life of properly maintained toll roads should outlast the concession term.
- Counterparty Risks: in certain toll road structures, investors will have to consider the ability for a counterparty to make timely and ongoing payments throughout the term of the project. An availability payment structure requires the public sponsor to make a long-term commitment to provide annual payments for the operation and maintenance of a project, subject to certain “availability” performance standards. By contrast, a revenue risk toll concession requires the concessionaire to assume the risks of revenue generation. Investors purchasing a toll road asset under an availability payment structure will consider the public sponsor’s ability to make payments to the concessionaire, as well as the performance payment regime.
- Revenue Considerations: assessing revenue considerations is one of the most important factors of valuing a toll road. Investors will primarily consider two overarching aspects with respect to the ability to generate revenue for a toll road: (1) the volume of traffic, and the (2) ability to raise toll rates. Uncertainty surrounding the ability to generate certain traffic levels and/or raise toll rates over time contributes to investor’s view of risk when valuing a toll road asset. Investors valuing a brown field toll road asset will consider both aspects with the benefit of a demonstrated history of traffic, which will reduce risk surrounding the forecasting of future revenue compared to a green field valuation with no operating history.
- Operating Cost Considerations: when valuing operating costs for a toll road, investors may consider the age of the road and associated equipment, its geographic location and typical weather conditions, terrain, and toll collection approach. Deferring ongoing maintenance may shorten the asset’s life and investors will consider the level of future funding that is needed to ensure proper road preservation. Also important is the concessionaire’s contractual structure for handling operations and routine maintenance. Under a concession structure, the concessionaire may outsource the operations and maintenance of the toll road to a third-party who specializes in providing these services. Investors will consider both the actual level of operation and maintenance costs from the history of operating the asset as well as the operating and maintenance regime.
- Renewal Costs Considerations: investors will seek to understand the expected economic life of the toll road asset, and the level, if any, of additional capital improvement funding that is needed to be made to ensure the asset is maintained to proper standard. These capital improvements would ideally be paid with revenue generated from the asset. If additional funds are needed for capital improvement requirements, investors will consider these additional needs when determining the price paid for the asset and the overall funding mix compared to the remaining term of the concession. Asset conditions will impact the level of future capital improvement needs, operating and maintenance (O&M) costs, ability to generate revenue, and future funding needs.
- Handback Requirements: investors will also consider the handback requirements to the public sponsor at the end of the concession term. Handback requirements typically surround the asset’s return to the public sector in a certain condition (i.e., properly maintained throughout the term of the contract). Asset handback requirements that are not met include financial penalties to the investor.
Investors entering into a concession agreement will consider primary key value drivers, such as those described above, as well as other structuring, legal, and financial considerations to develop projections for the amount of cash flow that the asset will potentially generate over the remaining term of the concession. The price that an investor would be willing to pay is determined based on the expected future level of cash generation. In many cases, there is no terminal value calculated on a concession, as once the concession term has expired, the asset is handed back to the public sector.
To determine cash flow available for equity distributions, investors will develop a forecast of revenue generation from tolling or availability payments and deduct expected future O&M expenses, renewal and rehabilitation costs, taxes, principal and interest on debt, and any other ongoing obligations as part of the cash flow waterfall on an annual basis. Historical results will be highly beneficial to investors for forecasting future needs. The bottom-line amount on an annual basis represents distributions to the equity investors for purchasing the asset, and the expected amount of future distributions will inform investors of the current price they are willing to pay.
The key value driver considerations as discussed above as well as other risks to a project as determined by an investor will determine the discount rate that an investor utilizes to discount future cash flows to a present value to assist in informing the investor of the price that should be paid for the equity ownership in the asset. All else equal, a higher discount rate to future cash flows will result in a lower present value of future cash flows and vice versa. The present value of future cash flows is the basis for an investor’s price for the equity in a project. Investors will determine their optimal capital structure to purchase the equity in a concessionaire.
The capital structure for a concessionaire or investor purchasing a toll road concession will be much different from a public owner and operator of a toll road, given the private sector goal of profit maximization. Investors of toll road asset will maximize earnings by leveraging the asset as much as lenders and structural project features will allow, as additional debt in lieu of equity maximizes financial return on the asset. For instance, investors purchasing a toll concession may purchase the original equity in the concessionaire in the transaction, and in many cases refinance outstanding debt to leverage the asset to the optimal capital funding mix. The example below illustrates the refinancing arrangement for the Chicago Skyway as detailed by FHWA (31).
The Chicago Skyway was purchased by Calumet Concession Partners LLC in 2016. This example demonstrates Canadian pension funds’ appetite for mature U.S. infrastructure assets that have completed construction and have a demonstrated operating history – thus reducing risk to a level commensurate with a pension funds’ appetite. The original capital structure included a combination of equity and debt as shown below. In 2005, the structure was refinanced to include additional debt to leverage the asset. The 2016 sale to Calumet Concession Partners LLC totaled $2.8 billion including the sources of funding provided below. The term of the concession did not change when Calumet purchased the original equity stake in the concessionaire.
Original capital structure: $882 million equity; $948 million bank loan
2005 refinancing: $510 million equity; $961 million capital appreciation bonds; $439 million current interest bonds; $150 million subordinate bank debt
2016 sale: $1.5 billion equity; $1.26 billion bank debt
Implications for Establishing Asset Value
The above discussion has several important implications for the use of the market perspective for valuing transportation assets. These include:
- Where market value can be determined, it incorporates consideration of the cost of an asset, its current condition, and a range of other factors.
- It is often feasible to establish market value for assets that can be readily transferred, such as vehicles and equipment.
- For fixed assets it may be possible to establish a market value for a facility encompassing multiple assets by observing the price established for a proposed or actual privatization concession.
- Where a market value has been established it is specific to a given asset or facility and cannot be readily applied to other assets without accounting for the key value drivers. Examples of these drivers are discussed above for the case of a toll road concession.
- The financing of a transaction is extremely important in the case of large-scale transactions such as toll road concessions. This complicates the process of using the price of such a transaction for asset management applications where details concerning how work is financed are largely immaterial.
Calculation Steps
The process for applying the market perspective to asset valuation is summarized below.
- Step 1 – Establish Whether a Competitive Market Exists:
Evaluate whether a market exists for a given asset or group of assets. A market is likely to exist in cases where the asset can be readily transferred between owners, such as for vehicles and equipment. A market may exist if a private concession has been proposed or implemented. The market can be competitive if there are multiple potential buyers and/or multiple sellers in the market.
- Step 2 – Identify Applicable Assets:
Specify the specific assets for which a market price can be established. In the case where value is established through the price of a private concession, the price may be specific to a small group of assets – e.g., the pavement and bridges that are part of a toll facility.
- Step 3 – Adjust the Market Price for Inflation:
If the market price is not current, it should be adjusted for inflation. See Appendix 4.B for a discussion of the treatment of inflation. Once the market price has been adjusted, it represents the current value for the selected assets.
- Step 4 – Value Other Assets Using the Replacement Cost Method:
Where market price can be calculated for only a subset of the assets being included in a calculation, the initial value for other assets should be calculated using the current replacement cost approach.
Overview
The economic perspective differs significantly from the cost and market perspectives due to the way it compares the value of an improvement to a baseline. With the other perspectives baseline values are established, but with the economic perspective the baseline is not a starting point for future valuation via treatments or depreciation. Instead, the baseline is compared to the improvement value, or the total net incremental value to the public brought about by building a given asset or facility relative to not doing so. Depreciation and the impact of treatments are inherently included within the user and externality values. Furthermore, unlike the case of the other perspectives, the economic perspective incorporates both user and non-user impacts, positive and negative.
With the economic perspective, historic data on the use and economic value of an asset mark trends for the current economic value. With this perspective, the current asset is presented as the baseline, and any changes to the asset – such as maintenance, realignment, or decommission – are given value relative to the benefits and costs they provide to the public. In the cases of roadway construction or decommission, an asset’s value is assessed by comparing the total future opportunities an asset generates with the opportunities created by alternative land uses.
Establishing Value
Although the methods for obtaining the benefits and costs can be complicated, the outcome is simple. If the public experiences a net gain in value due to the roadway investments, then these investments are worthwhile. While economic theory provides a reasonable methodology for assessing the net value of these investments, the challenge is determining how the public values changes to roadways or other transportation assets.
Members of the public do not value a transportation asset equally, nor do they prioritize the same value categories. The size and geographical range of the impacted community is unique for each asset. As the significance of the transportation system increases the impacted range also increases. For example, the people and businesses who gain from changes to an interstate freeway – both current and potential future users – could live in the same city or they could live a thousand miles away from each other. Meanwhile, only the residences located close to the freeway will experience firsthand the negative impacts of noise and emissions, especially if those externalities lower property values.
Establishing the value for improvements to a transportation asset begins with recognizing its role in people’s lives and business activities. Transportation assets allow people and goods to travel faster, safer, and more conveniently. They enhance route options via improved network connectivity and create new links to destinations previously inaccessible or at least for which access was cost prohibitive. Bridges, especially major ones, are special cases because they significantly enhance connectivity and overcome physical transportation barriers. Highways also create a secondary benefit by establishing public right-of-way that allows utilities (e.g., energy, water, and communications), to expand connectivity and capacity for communities.
An asset’s total economic value accounts for all uses and location characteristics that could positively or negatively impact people and businesses. The scale of benefits is determined by the volume of vehicular travel in the case of highways and person travel for transit. This volume is relatively easy to estimate from traffic counts. Building upon the traffic counts, sophisticated models, such as travel demand models, predict how physical changes to a facility or network impact travel characteristics such as volume, frequency, vehicle occupancy, and trip scheduling.
Principles of Economic Valuation
Several important principles are applied in all economic valuations. First, it is important to identify the potential effects of a project attributable to its costs. A clear definition of the impacts from the project is crucial for correctly estimating the benefits. This serves to avoid double counting the project’s benefits and disbenefits. Another principle of economic valuations is to compute the present value of future costs and benefits, enabling comparisons with a common basis of understanding. The discount rate, which brings future values into present value, can have a non-trivial influence on the analysis of different projects, depending on the timing and magnitudes of the project impacts. As a result, the selection of the discount rate becomes an important policy decision and consideration for sensitivity analyses. These and other issues are discussed more fully in Appendix 4.A.
Comparative Contexts for Asset Management
Asset management assessments differ from capital projects involving new construction, but still require a comparison to reveal their value. Asset value may need to be calculated in several different contexts including:
- Maintenance activities for one or more assets
- Physical changes to a particular asset that could impact its future uses
- System-wide assessments for an entire class of transportation assets (e.g., Interstate).
Maintenance Activities. An economic measure of value can assess the difference in value obtained by users at different levels of service for roadway surfaces or safety features. The user value is measured by comparing an enhanced level of maintenance against the current conditions. Principal measures of user value are travel speeds and vehicle operating and maintenance costs, which increase with poor road quality. There is an extensive collection of literature studying the impacts of road quality on users (32). However, in practice, the incremental economic value of improved maintenance is relatively low compared to the value measured via the cost approach.
Physical Changes. This second case is the most common form of economic analysis since it involves an evaluation of physical changes to an asset that affect its use. Changes include user-oriented improvements such as capacity (e.g., widening, overpasses, and truck lanes), operational improvements (e.g., interchange improvements, shoulders, and auxiliary lanes), and access (e.g., decommissioning, one-way streets, ramps) that aim to alleviate congestion, improve safety, or serve other agency goals. Economic valuations of such physical changes rely on forecasted changes in traffic patterns compared to a baseline that accounts for future uses under the current design. The value of these physical changes is estimated by differences in benefit categories (e.g., time savings, operating costs) over the life of the projects.
System-Wide Assessments. The value of an asset can be evaluated from a system-wide perspective by examining the next best alternative road class. However, this is usually a contrived exercise, and offers limited benefit outside of the theoretical. Consider the value of a state’s major arterial facilities. From an aggregated asset perspective, the next best option would be the minor arterials. Each type of roadway has a common set of characteristics, including average travel speeds per mile, intersection crossings and signals, and potential levels of normal traffic congestion. In this hypothetical case, the value of the major arterial is derived from the differences in value categories between the major and minor arterials. Since major arterials permit faster speeds, their value is expected to be higher, provided that the value of this reduced travel is not overcome by potentially increased travel cost or crash risk. This same approach could be applied for other roadway classes too. The use of local neighborhood roads in a car can be compared with an option to ride a bike or walk to a destination. These with- or without- asset evaluations require data on the use of a facility as well as data on opportunities created by eliminated vehicle use.
Calculation Steps
The process for applying the economic perspective to asset valuation is summarized below.
- Step 1 – Define the Assessment Scope:
Establish the set of assets to be analyzed. Define the with- and without-project contexts. Demarcate the breadth of the analysis geographically and temporally.
- Step 2 – Identify Potential Impacts:
Select the variables, or categories of impact, which will have an impact on the user and non-user benefits and disbenefits. Consider the characteristics of the asset, its users, and the community surrounding it. Options include travel time, vehicle operating costs, safety, pollution, asset maintenance, and wider community impacts, among others.
- Step 3 – Evaluate and Collect the Data:
Assess the data necessary to measure the potential impacts. Understand the trade-offs between stronger data collection and collection costs. For the chosen datasets, convert the impact categories into impact factors and impact value per unit.
- Step 4 – Project System Use:
Use current and historic traffic or passenger counts to understand the trends in the volume of vehicles and passengers. Predict the use of the system with and without investment, such as through use of a travel demand model.
- Step 5 – Calculate the Economic Value:
Using the output of the demand models and the impact data, weigh the benefits and costs of the with- and without-project contexts. Monetize impacts and apply a discount rate to bring benefits and costs into present value, and, if assessing a large transportation asset, account for the residual value at the end of the time period. Compare the two project scenarios to understand the value of the proposed changes.
The following are hypothetical examples illustrating application of the steps described in Section 4.2.
For pavement an agency decides to base its calculation of initial asset value on reconstruction cost using pavement lane miles as the unit of measure. Table 4-2 shows the data obtained to compute a unit cost for pavement in millions of dollars per lane mile for a given subtype and network. The table lists data for a set of pavement reconstruction projects. For each it shows the project year, quantity of pavement reconstructed in lane miles, project cost in year of expenditure dollars, and project cost in 2020 dollars. Project costs were inflated to 2020 costs using the Engineering News Record (ENR) Construction Cost Index.
Table 4-2. Example Data for Past Pavement Reconstruction Projects
| Project | Year | Description | Cost - Year of Expenditure ($M) | Cost - 2020 ($M) | Lane Miles (LM) | Unit Cost (2020 $M/LM) |
|---|---|---|---|---|---|---|
| 1 | 2010 | Route 80 MP 1.9 | 52.6 | 68.5 | 24.0 | 2.9 |
| 2 | 2016 | Route 84 MP 0.6 | 13.5 | 15.0 | 3.6 | 4.2 |
| 3 | 2007 | Route 92 MP 2.6 | 27.0 | 38.9 | 10.2 | 3.8 |
| 4 | 2011 | Route 101 MP 4.7 | 35.6 | 45.0 | 6.3 | 7.1 |
| 5 | 2005 | Route 101 MP 7.1 | 180.0 | 277.2 | 32.0 | 8.7 |
| 6 | 2014 | Route 104 MP 18.6 | 25.7 | 30.1 | 4.2 | 7.2 |
| 7 | 2009 | Route 104 MP 19.9 | 12.0 | 16.1 | 1.8 | 8.9 |
| 8 | 2017 | Route 680 MP 5 | 42.1 | 45.0 | 19.6 | 2.3 |
| 9 | 2013 | Route 680 MP 12 | 28.3 | 34.0 | 8.0 | 4.3 |
| 10 | 2018 | Route 780 MP 15.5 | 28.0 | 29.0 | 9.2 | 3.2 |
| Total | 598.8 | 118.9 | 5.0 |
The result is a unit cost of $5.0 million per lane mile. However, in reality there is a significant difference in costs between the different projects, with most projects in the range of $2 to $4 million and a small number of more expensive projects. This may suggest a need to group pavements by system or surface type to better account for this variability.
An agency decides that to maintain consistency with its financial reporting, the agency should use historic costs rather than current replacement cost. However, historic cost data are not consistently available. Thus, the agency decides to use the Wooster Method to estimate historic costs. Table 4-3 shows the application of this method for a selected set of assets using unit cost of $5 million per lane mile (as obtained in Example 4-1). The unit cost developed as described in Example 4-1 is applied and deflated to estimate historic costs. In this hypothetical example the total replacement cost is $3.9 billion in constant 2020 dollars and $2.0 billion in year of expenditure (historic) dollars.
Table 4-3. Estimation of Historic Costs of Pavement Reconstruction
| Route | Lane Miles (LM) | Year Constructed | 2020 Cost ($M) | Historic Cost ($M) |
|---|---|---|---|---|
| 11 | 96 | 2001 | 480.0 | 265.5 |
| 11 | 128 | 2004 | 640.0 | 397.1 |
| 22 | 72 | 1989 | 360.0 | 144.9 |
| 22 | 192 | 1996 | 960.0 | 470.5 |
| 33 | 32 | 2000 | 160.0 | 86.8 |
| 44 | 44 | 2003 | 220.0 | 128.4 |
| 44 | 8 | 1997 | 40.0 | 20.3 |
| 55 | 128 | 1990 | 640.0 | 264.1 |
| 66 | 28 | 2001 | 140.0 | 77.4 |
| 77 | 52 | 1999 | 260.0 | 137.4 |
| Total | 3,900.0 | 1,992.7 |
A transit agency has a fleet of over-the road transit buses purchased at different times from the same manufacturer. The agency seeks to establish the value of these buses using market value. Table 4-4 is a list of used coach buses from a selected manufacturer available for sale from an online bus reseller. It shows the age, mileage and price of each bus offered for sale.
Table 4-4. Over-the-Road Coach Buses Available for a Selected Manufacturer and Reseller
| Bus | Age (years) | Mileage | Prices ($) |
|---|---|---|---|
| 1 | 7 | 650,000 | 239,900 |
| 2 | 9 | 181,000 | 234,900 |
| 3 | 12 | 288,000 | 149,900 |
| 4 | 14 | 305,000 | 204,900 |
| 5 | 14 | 399,899 | 239,900 |
| 6 | 15 | 350,000 | 69,900 |
| 7 | 18 | 550,567 | 32,500 |
| 8 | 22 | not listed | 25,000 |
The agency uses the data in the table to construct a simple linear model for predicting the price of a used bus. In this case, price is predicted as a function of age using the following relationship:
Price = 377,035 - 16,391 * Age
Figure 4-2 shows the resulting model.
Note that alternative models were tested including both mileage and age, and substituting mileage for age. In this case the age-based model provides the best fit. In practice price may depend on a number of age, mileage, and other variables.
An agency is interested in using asset value to help prioritize reconstruction of a set of bridges to improve resilience. After discussing the cost, market and economic perspectives on asset value, agency leadership determines that the economic perspective is needed for this application. This perspective can help compare the benefits to society of reconstructing different bridges. Agency staff adapt the bridge screening approach established in FHWA’s National Bridge Investment Analysis System (NBIAS) to estimate asset value (32).
The approach used by NBIAS is to calculate the benefit of a bridge as the savings in travel and operating costs relative to that which would be incurred if all vehicles were detoured around the bridge. The calculation is made for autos and truck, and summed over time, applying a discount rate. The approach utilizes data available for U.S. highway bridges in the National Bridge Inventory (NBI) along with a small number of additional parameters. The following equations detail the calculation:
\begin{align*} B_a &= 365.25*T [ \frac{\tau}{100}(L C_l^t + \frac{L}{v_d} C_h^t) + (\frac{100-\tau}{100})(L C_l^t + \frac{L}{v_d} C_h^c)] \\ B &= B_a \sum_{i=1}^{N} \delta^{(i-1)} \end{align*}
where:
This section provides examples of “emerging,” “strengthening,” and “advanced” practices with respect to calculation of initial asset value. Maturity levels are defined for each of the four approaches defined in the guidance. In the table an emerging practice is one that supports the guidance with minimal complexity, an advanced practice illustrates a “state of the art” example in which an agency has addressed some aspect of the asset value calculation in a comprehensive manner, and strengthening practice lies between these two levels.
Unit replacement costs are established by asset class/component using expert judgement and/or industry defaults.
Unit replacement costs are established through a one-time analysis of project data and updated in subsequent years based on inflation.
Unit replacement costs are established through a well-documented process that includes: analysis of project data; assessment of how assets should be grouped for analysis (e.g., by system, material and/or surface type); and a defined update cycle (e.g., once every 1 to 2 years).
Neither historic costs nor asset age can be reliably obtained at an asset level. Overall expenditures by work type and system are used as the basis for calculating asset value without relating expenditures to specific assets.
An asset inventory is available detailing asset age. Historic costs are not reliably tracked by asset but can be estimated using unit replacement costs and asset age
Actual costs of construction/asset purchases are tracked by asset.
Market value is estimated based on expert judgement and/or industry defaults.
Market value is established through a one-time analysis of asset resale or other data and updated in subsequent years based on inflation.
Market value is established through a well-documented process that includes: analysis of asset resale or other data; assessment of how assets should be grouped for analysis (e.g., by system, material and/or surface type); and a defined update cycle (e.g., once every 1 to 2 years).
Calculations of economic value rely on estimates of detour distance and speed to estimate changes in user costs from addition or removal of an asset, but do not attempt to quantify the impact of changes in travel demand.
Calculations of economic value rely on estimates of detour distance and speed to calculate changes in user costs from addition or removal of an asset. The elasticity of travel demand is used to estimate changes in traffic volumes.
Calculations of economic value utilize travel demand models to quantify impacts of potential changes to the network from addition or removal of an asset.
An important part of performing the asset value calculation is accounting for asset treatments and their effects. Treatments are important in two basic ways:
- It is important to consider what treatments are typically performed on an asset to determine an asset’s useful life and “residual value,” or value when an asset reaches the end of its useful life.
- In some cases, one may wish to specifically include additional treatments in the asset value calculation besides asset acquisition/construction and reconstruction. This is particularly important if one is predicting future asset value.
To calculate asset value, one should establish what treatments are performed on an asset. An asset lifecycle strategy describes the different treatments that are typically performed on an asset following its initial construction or acquisition. Defining a lifecycle strategy is consistent with best practice in TAM. Also, State DOTs are required to define lifecycle strategies for pavements and bridges in their NHS TAMP.
At a minimum, basic information on what asset treatments are typically performed on an asset is useful in establishing asset life and residual value as described further in subsequent subsections of this chapter. For instance, for the purpose of valuing service vehicles, one would set the life of the asset assuming that various treatments are conducted based on the asset’s lifecycle strategy, such as routine maintenance and replacement of brakes, tires and other vehicle components.
For certain applications it may be necessary to go a step further, and include the costs and effects of various asset treatments explicitly in the asset value calculation. This is particularly important if the intended application of the asset value calculation is to predict future asset value. In this case one may wish to account for what treatments are expected to be performed, and may wish to compare treatment strategies. In this case there are two reasons may wish to include a given treatment in the calculations:
- Specifying the Impact of Treatments on Remaining Asset Life. For some complex assets, such as pavement and bridges, treatments may be performed – short of outright replacement of the asset – that have a significant impact on the remaining asset life. For instance, if a pavement is overlayed or a bridge is rehabilitated, its useful life is expected to be much longer than if these treatments are not performed. In these cases, incorporating past treatments may yield a more accurate calculation of current asset value – if sufficient data are available to support the calculation.
- Demonstrating Effects of Treatments on Future Value. If the asset value calculation is being performed to demonstrate the effects of a given treatment, then the treatment needs to be accounted for in some manner to show how the value changes if the treatment is performed. For instance, one might calculate future asset value with and without performing the treatment.
Figure 5-1, adapted from the Edgerton’s discussion of this topic (12), illustrates the importance of considering renewal treatments for certain assets, referred to by Edgerton as “cyclical maintenance assets.” This figure shows three lines illustrating the value of an asset over time. The jagged line in the figure below shows asset value if renewal treatments are explicitly modeled: these add value and add life to the asset. The straight upper line shows how asset value is calculated if the effect of renewal treatments is approximated through a revised estimate of asset life. In this case, asset treatments are not explicitly modeled. The lower line is demonstrably incorrect. In this case, renewal treatments are not modeled, but the asset life has not been modified to account for these treatments. This results in systematic understatement of asset value.
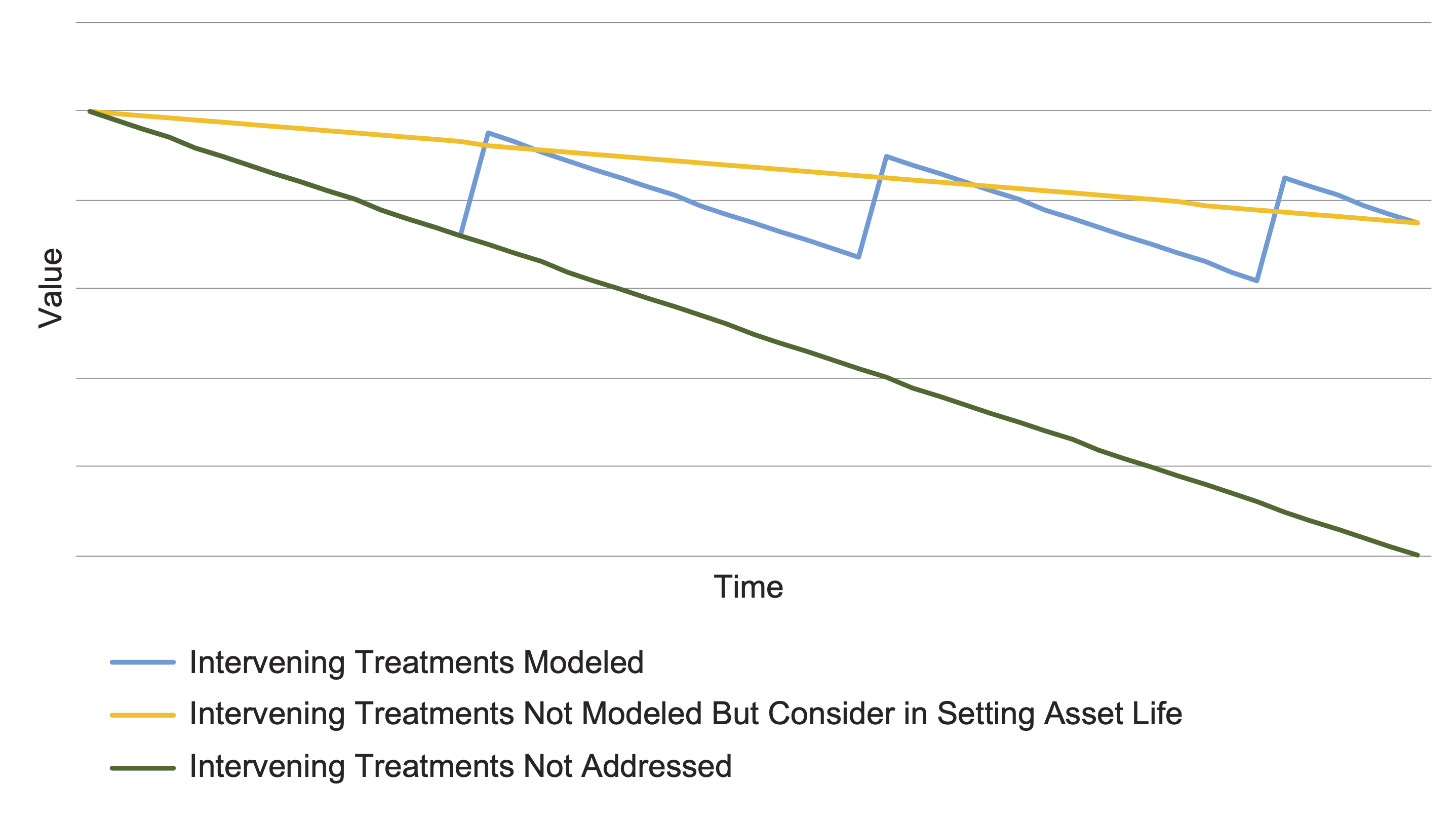
To determine what treatments to model it can be helpful to review multiple sources, such as guidance on what treatments are recommended for an asset, models in an agency’s management systems, and the data an agency actually tracks on its treatments. This is complicated since the same treatment may be represented in different ways between different organizations and/or systems.
For other applications where the goal is to calculate current asset value, it is generally not necessary to explicitly account for all of the different treatments that have been performed on an asset in the past. It is recommended that defining additional treatments be avoided in this case if possible. However, one may wish to consider additional treatments if value is based on historic costs, or if the depreciation approach is based on the actual time since the last treatment. Depreciation is discussed further in Chapter 6.
For each treatment that is modeled one must establish how much the treatment costs and what effect the treatment has on an asset. The approaches described in Chapter 4 for calculating replacement costs are equally applicable to calculating the cost of other treatments. Generally speaking, the calculation of treatment costs should be made in today’s dollars (constant dollars), removing the effects of inflation from the analysis. This approach allows for directly comparing costs incurred at different times. If calculations are made in current rather than constant dollars, one must be careful to state the year of the expenditure and avoid comparing costs in different years without inflation adjustments. However, in the case that one is basing asset value on historic costs all costs should be expressed in year of expenditure dollars.
Concerning treatment effects, the most straightforward case to consider is that the treatment has the effect of restoring the asset to “like new” condition, resetting its age to 0. Alternatively, a treatment might extend the life of the asset and/or improve its conditions. Both of these effects can be translated into a change in the effective age of the asset. If the impact of the treatment cannot be translated into a change in condition or effective age then it should not be explicitly considered.
When considering treatments and their effects, a key issue is how assets have been componentized. If a complex asset is represented using components, then this may simplify the specification of treatment effects, and allow for the consideration of additional treatments. For example, a common treatment for a bridge is to rehabilitate or replace the bridge deck, which resets the age of the bridge deck but may not impact the age of the bridge superstructure or substructure. If a bridge is represented in components consisting of a deck, superstructure and substructure, then the effect of a deck replacement can be easily modeled: it resets the age of the deck to 0 and improves its condition to a “like new” condition. If one is modeling the overall bridge, then the effect of a deck replacement is more difficult to ascertain. One can approximate the effect in this case, or simply assume that deck replacement occurs on a regular cycle and not attempt to model this treatment.
Once the analyst makes a decision about what treatments to explicitly model and what treatments are assumed to occur over the life of an asset, they can then establish the asset’s expected useful life. Asset life is an important parameter for the depreciation calculation described in Chapter 6.
The goal here is to determine how long the asset would be expected to remain in service provided:
- An asset is removed from service either when it is more cost effective to replace the asset or when it is obsolete;
- The treatments that are assumed to occur in the analysis actually do occur, including planned maintenance, cyclical treatments that are needed to achieve the asset’s useful life, and any other treatments that may impact the life of the assets if they are omitted; and
- The life-restoring treatments distinguished from general maintenance are not assumed to occur, as their contributions to asset value and life will be accounted for separately.
The above criteria have some important implications. One is that we are not concerned with how long an asset would remain in service in the abstract case that no treatments are ever performed on an asset. Instead, we would like to know what the useful life is given treatments such as routine maintenance are performed. But this means that estimates of useful life are contingent on the assumed set of treatments performed on an asset, also called the agency’s lifecycle strategy for the asset.
Another implication of the above criteria is that it is completely feasible for an asset to remain in service past its useful life. This may occur because it is still cost effective to maintain a specific asset, or because it has simply not been feasible to replace the asset and it continues to be maintained despite the fact that a replacement may be more cost effective.
Assets of historical significance are unique in this manner, for they are maintained beyond the useful life that would otherwise be defined for them. These assets require special treatment. Specific estimates may be required of the time until major rehabilitation action is required to retain such assets in service – or such assets can be componentized.
Various references are available which summarize typical useful lives of transportation assets and provide techniques for calculating agency-specific values. Two references are of particular note. Volume 1 of NCHRP Report 713 (18) is a guidebook for measuring the life expectancy of transportation assets. This report details how to define asset end-of-life, describes quantitative approaches for establishing asset life, and presents typical values for selected asset classes.
The OECD manual Measuring Capital (11) summarizes approaches for estimating useful lives for the purpose of calculating asset value, including techniques, such as development of Winfrey Mortality Functions and Weibull distributions. It also presents typical values for different asset classes based on a review of the literature. One application described in this manual uses an assumed distribution to approximate the age distribution of an asset inventory where detailed data are unavailable. For TAM applications it is assumed that sufficient data are available to determine the age distribution of an asset inventory, but the reader should consult the discussion in Chapter 12 of Measuring Capital where this is not the case.
Table 5-1 below summarizes typical useful lives for transportation assets based on NCHRP Report 713, Measuring Capital, NCHRP Synthesis 371 (19), and FTA guidance for vehicles (33). As noted above, all of the assumptions regarding asset life are assumed to incorporate a given treatment strategy. One should review the assumptions and their own data carefully when performing an analysis.
Table 5-1. Typical Useful Life Values for Transportation Assets
| Asset Class | Component | Typical Useful Life (years) | Notes |
|---|---|---|---|
| Pavement | Overlay - Asphalt | 11-20 | NCHRP Report 713 Vol. 1 (summary of the literature) |
| Overlay - Concrete | 20-34 | ||
| Full Depth - Asphalt or Concrete | 50 | ||
| Bridges | Deck | 58-79 | NCHRP Report 713 Vol. 2 (time to reach a rating of 3 or 4 based on model fit to NBI data) |
| Superstructure | 64-83 | ||
| Substructure | 59-78 | ||
| Culverts | Pipes | 50 | NCHRP Synthesis 371 (mode of survey results) |
| Box Culverts | 55-85 | ||
| Traffic Signals | Signal Head | 15 | NCHRP Report 713 Vol. 2 (time to reach a rating of 3 or 4 based on model fit to NBI data) |
| Structural Components (stell or aluminium) | 25-30 | ||
| Traffic Detector | 10 | ||
| Traffic Controller | 15 | ||
| Traffic Controller Cabinet | 20 | ||
| Lighting | Structural Components (steel or aluminium) | 25-30 | NCHRP Synthesis 371 (mode of survey results) |
| Ballast | 10 | ||
| Control Panels | 20 | ||
| Signs | Sheeting | 15 | NCHRP Synthesis 371 (mode of survey results) |
| Sign Posts (steel or wood) | 10-15 | ||
| Overhead Sign Structure | 30 | ||
| Sidewalks and Curbs | Asphalt | 10 | NCHRP Synthesis 371 (mode of survey results) |
| Concrete, Block or Brick | 20 | ||
| Vehicles | Automobile | 8 | FTA Useful Life Benchmark (ULB) Defaults |
| Cutaway Bus | 10 | ||
| Bus | 14 | ||
| Light or Heavy Rail Vehicle | 31 | ||
| Commuter Rail Coach or Locomotive | 39 | ||
| Ferryboat | 42 |
The final topic addressed in this portion of the asset value calculation is the determination of the residual value of the asset, or the value of the asset once it has reached the end of its useful life. Note this topic is addressed separately for the case where one calculates economic value, as discussed in Chapter 4. When one calculates value using a cost or market perspective, two basic approaches may be considered for determining this parameter: calculating the salvage value of the asset or calculating the cost to restore the asset to “like new condition.”
For assets that are completely replaced at the end of their useful life, the residual value should be based on the salvage value of the asset and may be 0. For instance, the salvage value for a vehicle might be set based on the price expected at auction. Assets that are discarded at the end of their life and not repurposed in some way have a salvage value of 0.
A different approach is recommended in cases where an asset is periodically rehabilitated and restored to a “like new” condition at a cost less than the initial construction or acquisition cost. In these cases, it is recommended that the residual value is equal to the difference between the cost of replacing the asset and the cost to restore the asset to “like new” condition at the end of its useful life. This approach is illustrated below in Figure 5-2. As demonstrated in the figure, this approach has the effect of restoring the value of the asset to that of a new asset when a complete rehabilitation treatment is applied. This method includes the aspects of an asset that do not depreciate or which depreciate very slowly in the residual value, such as foundations and earthworks, design, and land. Note that in this example it is assumed that the asset is restored to “Like New” condition. However, depending on the asset and treatment it may or may not be feasible to restore the asset to this condition.
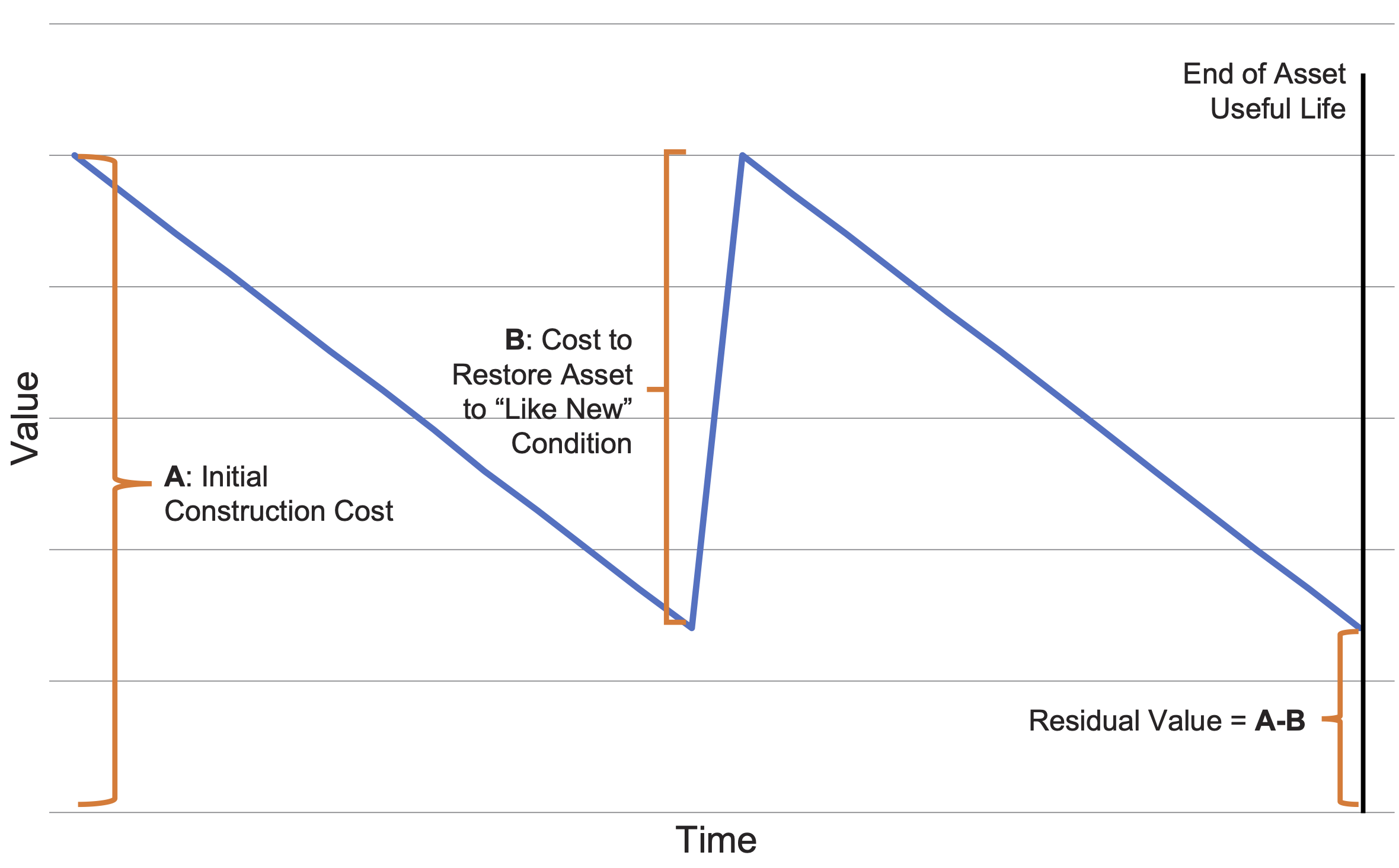
This section describes the specific steps involved in the four basic activities addressed in this chapter: identifying treatments; determining treatment costs and effects; determining asset useful life; and determining residual value.
- Step 1 – Review Treatment Data:
For each asset class and type of component being valued, review the asset lifecycle strategy and/or other available agency data to determine what treatments are typically performed on an asset class or component, and what treatment data are consistently tracked.
- Step 2 – Identify Mandatory Treatments:
Identify treatments that will be considered independently in the valuation calculation, in addition to the initial construction or acquisition of an asset. These include treatments that reset the asset age or restore an asset to “like new” condition.
- Step 3 – Select Potential Additional Treatments:
Determine whether additional treatments should be considered in the analysis. Consideration of additional treatments is typically unnecessary for calculating current asset value, but can be important for predicting future value. Treatments may be added to the analysis if they have some impact on asset remaining life or condition and if adding them to the analysis will help support TAM decisions. Any treatments not explicitly modeled are assumed to occur based on the agency’s lifecycle policy.
- Step 1 – Collect Data on Past Treatments:
Collect data on cost and treatment timing for each treatment being considered for each asset class and subcomponent. Data are not required for treatments that are assumed to occur and incorporated in the estimate of asset useful life.
- Step 2 – Assess Available Data:
Decide whether historic data are sufficiently detailed to support use of actual costs, or if unit costs will be used to estimate changes in value from past treatments. For most applications it is more practical to use unit costs. An exception to this is where value is being calculated for a specific asset (e.g., a toll road) based on historic costs.
- Step 3 – Develop Treatment Unit Costs:
Develop unit costs as described in Chapter 4, resulting in unit costs for each treatment.
- Step 4 – Determine Treatment Effects:
For each treatment determine the effect the treatment has on an asset. The effect can be specified in terms of the change in asset life or the change in condition. Condition changes are equated to asset life in calculating depreciation, as described in Chapter 6.
- Step 1 – Review Available Agency Data:
Collect and review records on when assets have been replaced. Ideally data on past replacements should be accompanied by information on what motivated the replacement.
- Step 2 – Review Defaults and Past Assumptions:
Review other sources of data for asset life assumptions, including information on treatments compiled as described in Section 5.2.1, past calculations performed by the agency (e.g., for previous TAMPs or financial reports), asset-specific analyses, the defaults listed in Table 5.2, and the TAM literature.
- Step 3 – Specify the Useful Life by Asset Class/Component:
Determine a useful life for each asset class and component being valued using either the agency’s data or the defaults. The useful life should be developed assuming treatments occur according to the agency’s lifecycle strategies.
Refer to NCHRP Report 713 and Chapter 13 of OECD Measuring Capital for more discussion of advanced approaches for establishing asset useful life.
- Step 1 – Classify Assets and Components:
For each asset class and component being valued, establish whether or not the asset is periodically rehabilitated or renewed using treatments that differ in cost from the initial purchase or construction of an asset. This determination depends on the nature of the treatments performed on the assets and the determination of which treatments are being modeled.
Complex assets such as pavements and bridges are periodically rehabilitated or renewed. However, the analyst has the choice concerning whether to consider rehabilitation/renewal treatments or assume these occur according to the agency’s lifecycle strategy.
- Step 2 – Calculate Salvage Value:
For assets not subject to periodic rehabilitation or renewal calculate the residual value as the salvage value of the asset, or the value obtained for an asset that has reached the end of its useful life and is being replaced. Refer to the OECD document Measuring Capital for discussion of how to establish this value for complex cases when the distribution of asset useful life cannot be easily approximated.
- Step 3 – Calculate the Cost Difference:
For assets that are subject to periodic rehabilitation or renewal, calculate the residual value as the difference between the cost of initial purchase or construction and the cost of asset rehabilitation or renewal.
The following are hypothetical examples illustrating application of the steps described in Section 5.2.
A highway agency needs to calculate asset value for pavements and bridges to support development of its TAMP. The agency is interested in exploring two different approaches to asset valuation, both of which utilize replacement cost for the calculation of initial value: a simplified approach in which only asset construction/reconstruction is considered in the calculation, and a more comprehensive approach that more accurately reflects the impacts of rehabilitation and preservation treatments on asset value.
The agency starts by reviewing different pavement and bridge treatments performed by the agency. This process is complicated by the fact that different terms are used for describing asset treatments in different systems. The agency reviews existing TAMPs to determine how different treatments have been represented by other agencies. Table 5-2 provides an example of the mapping of different treatments between pavements and bridges based on data presented in the Louisiana Department of Transportation Development (LADOTD) TAMP (34). The table shows, for pavements and bridges, the five work categories described by FHWA in its TAMP requirements, corresponding work types used when reporting data for federally-funded projects in the FHWA Financial Management Information System (FMIS), and the treatments actually considered by the agency’s asset managers. As shown in the table, for any one of the FHWA work categories there may be between zero and four corresponding different work types in FMIS. The work types in FMIS may map to a number of different specific treatments.
Table 5-2. Example Mapping of FHWA Work Categories, FMIS Work Types and Agency Treatments
| FHWA Work Category | FHMIS Work Types | TAM Treatments |
|---|---|---|
| Pavement | ||
| Initial Construction | 01-New Construction Roadway | New Roadway Construction |
| Maintenance | N/A | Seal Joints and Cracks Polymer Surface Treatment |
| Preservation | 05-4R Maintenance Resurfacing | Microsurfacing Thin Overlay Medium Overlay In Place Stabilization |
| Rehabilitation | 06-4R Maintenance Restoration/Rehabilitation | Structural Overlay Minor Rehab Major Rehab |
| Reconstruction | 03-4R Reconstruction - Added Capacity 04-4R Reconstruction - No Added Capacity 07-4R Relocation | Reconstruction Unbonded Concrete Overlay |
| Bridge | ||
| Initial Construction | 08-Bridge New Construction | Bridge New Construction |
| Maintenance | N/A | N/A |
| Preservation | 40-Special Bridge 47-Bridge Preventative Maintenance 48-Bridge Protection 59-Bridge Deck Resurfacing | Painting Deck Scour Mitigation Cleaning, Refurbishing or Replacing Service Elements |
| Rehabilitation | 13-Bridge Rehabilitation - Added Capacity 14-Bridge Rehabilitation - No Added Capacity | Re-Decking Widening Paint with Major Structural Steel Repairs Scour Mitigation with Major Substructure or Other Major Bridge Work |
| Reconstruction | 10-Bridge Replacement - Added Capacity 11-Bridge Replacement - No Added Capacity | Remove Existing Structure Replace Existing Structure |
All of the specific agency treatments listed in the table could conceivably be included in the asset valuation calculation. Adding treatments supports a more detailed and potentially more accurate calculation of how asset value varies over time, but entails quantifying more data.
Table 5-3 shows the results of the agency’s assessment, indicating which treatments the agency will include in the asset value calculation using each approach. For the comprehensive approach the agency elects to include a number of additional treatments, given these improve asset condition and result in shortening asset life if needed treatments are not performed.
Table 5-3. Treatments Included Using Simplified and Comprehensive Approaches
| Treatment | Include in Value Calculation | Notes | |
|---|---|---|---|
| Simplified | Comprehensive | ||
| Pavement | |||
| Construction | Yes | No | |
| Overlay | No | Yes | Includes thin and medium overlays |
| Other Maintenance and Preservation | No | No | Includes crack sealing, surface treatment, and microsurfacing |
| Rehabilitation | No | Yes | Includes structural overlay, minor rehab and major rehab |
| Reconstruction | Yes | Yes | |
| Bridge | |||
| Construction | Yes | Yes | |
| Deck Repair | No | Yes | |
| Other Maintenance and Preservation | No | No | Includes cleaning, element repairs, spot painting, and deck protection |
| Deck Replacement | No | Yes | |
| Superstructure Rehabilitation | No | Yes | Includes paint replacement and major steel repairs |
| Substructure Rehabilitation | No | Yes | |
| Rehabilitation | No | Yes | |
| Reconstruction | Yes | Yes | |
The agency described in Example 5-1 next quantifies the cost and effects of the different treatments. The agency uses treatment costs from its management system, together with a separate assessment of the cost of initial construction of a pavement or bridge performed as described in Chapter 4.
Treatment effects are established based on a combination of expert judgement and parameters from the agency’s management systems. Table 5-4 shows the resulting assumptions concerning treatment effects. For pavement, treatment effects are expressed in terms of a treatment’s impact on Pavement Condition Index (PCI). This is an agency-specific measure of pavement condition expressed on a scale from 0 to 100. Pavement treatments have the effect of resetting pavement age and returning PCI to 100, setting PCI to a specific value, or increasing PCI by a specified amount.
For bridges treatment effectives are expressed in terms of a treatment’s impact on the deck, superstructure, and/or substructure ratings defined in the NBI. These are expressed on a 0 to 9 scale, with 9 representing the best condition obtained for a new bridge. Bridge treatments have the effect of resetting age and returning all ratings to 9, or setting one or more ratings to a specific value.
Table 5-4. Example Treatment Effects
| Treatment | Treatment Effect | |
|---|---|---|
| Simplified | Comprehensive | |
| Pavement | ||
| Construction | Age = 0, PCI = 100 | Age = 0, PCI = 100 |
| Overlay | None | PCI increases by 10 |
| Rehabilitation | None | PCI set to 90 |
| Reconstruction | Age = 0, PCI = 100 | Age = 0, PCI = 100 |
| Bridge | ||
| Construction | Age = 0, Deck/Super/Sub Ratings = 9 | Age = 0, Deck/Super/Sub Ratings = 9 |
| Deck Repair | None | Deck Rating = 6 |
| Deck Replacement | None | Deck Rating = 7 |
| Superstructure Rehabilitation | None | Superstructure Rating = 7 |
| Substructure Rehabilitation | None | Substructure Rating = 7 |
| Rehabilitation | None | Deck/Super/Sub Ratings = 7 |
| Replacement | Age = 0, Deck/Super/Sub Ratings = 9 | Age = 0, Deck/Super/Sub Ratings = 9 |
Based on the assessment of treatment effects, the agency establishes that with the more comprehensive approach it would be necessary to represent bridges at a component level, modeling the deck, superstructure and substructure of a bridge separately, given that several of the treatments have an impact on only one component.
The agency described in the previous example seeks to establish useful lives for bridges for the simplified and comprehensive cases outlined in the previous examples. The agency uses NCHRP Report 713 (18) for guidance. Following the approach described in this report, the agency first defines end-of-life criteria for its bridge components. The agency’s bridge managers recommend that when a deck, superstructure or substructure deteriorates to a rating of 5 on the 9-point NBI scale (classified as fair condition) the component has reached the end of its useful life, given the agency typically schedules rehabilitation work at this point to prevent the bridge from deteriorating into poor condition. Note that if the end of life was defined as the point when replacement of the bridge is required, then a lower rating value would be used as the definition for end-of-life. The agency uses the national defaults in Appendix B of Report 713 to estimate the time required for bridge components to deteriorate to a value of 5. These were developed using NBI data and implicitly include effects from routine maintenance. The national estimates in the report are:
- Deck – 42 years
- Superstructure – 48 years
- Substructure – 45 years
These values are used for the comprehensive case described in the above examples, in which bridges are represented at a component level, and rehabilitation treatments are included in the analysis.
For the simplified analysis the agency performs a separate analysis to determine a useful life for bridges assuming that maintenance, repair and rehabilitation work is performed consistent with the agency’s lifecycle policy. The agency reviews data on recent projects to establish a typical life, omitting projects where replacement was triggered by an external factor (e.g., the bridge crossed a roadway that was being widened to increase capacity). The agency compares this to the NCHRP Report 713 values for the time for component ratings to reach a value of 3, a point at which the agency would schedule replacement of a bridge. These are as follows:
- Deck – 79 years
- Superstructure – 83 years
- Substructure – 78 years
Based on review of agency data and other sources the agency establishes a useful life of 75 years for a bridge for the simplified case in which maintenance, repair and rehabilitation treatments are assumed to occur in a timely fashion over a bridge’s life.
A transit agency seeks to calculate residual value for its vehicles, facilities, track and equipment. Based on the guidance in Section 5-2, the agency calculates residual value for selected assets as shown in Table 5-5.
Table 5-5. Example Approaches for Calculating Residual Value for Transit Assets
| Asset Class | Subclass | Calculation Approach | Notes |
|---|---|---|---|
| Vehicles | Buses | Resale or auction value | Feasible when vehicles are auctioned or sold at the end of their useful life |
| Rail Vehicles | Scrap value | Assumes asset is used until it is scrapped | |
| Facilities | Administrative/Maintenance Facility | Difference between construction and rehabilitation cost | Complex assets that are rarely completely reconstructed |
| Passenger Facility | |||
| Infrastructure | Track | ||
| Structures | |||
| Power | 0 | Typically obsolete when replaced – minimal resale or scrap value | |
| Signals | |||
| Equipment | Service Vehicles | Resale or auction value | Feasible when vehicles are auctioned or sold at the end of their useful life |
| Other Equipment | Scrap Value | Assumes asset is used until it is scrapped |
This section provides examples of “emerging,” “strengthening,” and “advanced” practices for defining treatments and treatment effects. Maturity levels are defined for each of the four areas defined in the guidance. In the table an emerging practice is one that supports the guidance with minimal complexity, an advanced practice illustrates a “state of the art” example in which an agency has addressed some aspect of the asset value calculation in a comprehensive manner, and strengthening practice lies between these two levels.
Asset purchase or construction and reconstruction are included in the asset value calculations. Supplemental analysis is not performed to consider inclusion of other treatments.
An analysis is performed to determine what treatments to include in the analysis, and what treatments are assumed to occur based on the agency’s life cycle strategy. The analysis is conducted separately from establishing asset life cycle strategies.
An analysis is performed to determine what treatments to include in the analysis, and what treatments are assumed to occur based on the agency’s life cycle strategy. The analysis is conducted as part of the development of asset life cycle strategies and/or strategies are updated as appropriate following the analysis.
The analysis is limited to asset purchase or construction and reconstruction. Asset reconstruction is assumed to have the same cost and effect as initial construction.
Treatment costs are established through a one-time analysis of project data and updated in subsequent years based on inflation. Treatment effects are based on expert judgement or a one-time analysis.
Treatment cost and effects are established through a well-documented process that includes: analysis of treatment data; assessment of how assets should be grouped for analysis (e.g., by system, material, and/or surface type); and a defined update cycle (e.g., once every 1 to 2 years).
Asset useful life is estimated based on expert judgement and/or industry defaults.
A one-time analysis is performed to establish asset useful life based on analysis of historic data and/or asset models.
Asset useful life assumptions are based on models used in an agency’s management systems. The assumptions are periodically validated and updated through a well-documented process.
The analysis is limited to asset purchase or construction and reconstruction. Asset reconstruction is assumed to have the same cost and effect as initial construction (resulting in a residual value of 0).
A determination is made for each asset class and component concerning whether to calculate residual value based on salvage value or the difference between asset construction and reconstruction. Salvage values are established based on expert judgement.
A determination is made for each asset class and component concerning whether to calculate residual value based on salvage value or the difference between asset construction and reconstruction. Salvage values are established based on analysis of historic data.
Depreciation is defined as “the loss of value of an asset or class of assets, as they age.” (1). Depreciation represents the consumption of capital, or the consumption of the benefits of an asset. From an accounting perspective, the depreciation calculated over some period measures how much value of an asset has been “used up.” From the perspective of an asset manager, depreciation is a measure of how much closer an asset has moved toward the end of its useful life.
Depreciation is calculated when it is necessary to adjust an asset’s value over time. If an asset’s value is based on the initial cost of constructing or purchasing the asset, the value at a later point should be depreciated. If one is using a market or economic perspective to establish value, then it may not be necessary to calculate depreciation. In such cases, depreciation may need to be calculated if adjusting a prior calculation of asset value. However, it is preferable to simply revalue the asset by repeating the calculation of value performed as described in Chapter 4.
Depreciation is closely related to deterioration, or decline in the physical condition of an asset. Generally speaking, as an asset ages, its benefits are consumed and it deteriorates. However, the consumption of benefits (as measured by depreciation) and the decline in condition (as measured by deterioration) often occur at different rates. For example, in accounting it is common to assume accelerated depreciation, in which asset value is assumed to decline more rapidly for a new asset than an older one.
Below is an example illustrating how a deterioration curve can be used to calculate depreciation. Here value and condition are both depicted as a percentage of the value for a new asset. In this case, depreciation is assumed to be linear. Thus, the value of the asset decreases linearly from its initial value to its residual value. Condition of the asset follows an s-shaped curve (a logistic curve), in which the condition declines gradually near the beginning and end of an asset’s life, and more rapidly in the middle of its life. In this example it is further assumed that the asset is operated in the same manner over its entire life. Thus, the fact that physical conditions are declining more rapidly or slowly at different points in its life is immaterial: the key question is that of the remaining life of asset, which may need to be revised based on the asset’s condition. This example is representative of assets such as pieces of equipment that remain in service until the end of their life, and are used in the same manner generating the same benefits as long as they are safe to operate.
When the benefits derived from an asset depend upon its physical condition, the situation is different. In these cases, depreciation may be directly tied to deterioration, and therefore age is no longer an appropriate approximation. For example, for rail cars one might consider that as a vehicle ages riders suffer greater discomfort from riding on the vehicle and are more prone to experiencing delays in service. For pavement, user costs increase as pavement condition worsens. In such cases, the pattern of depreciation may better match the pattern of deterioration and a condition-based depreciation approach is best suited.
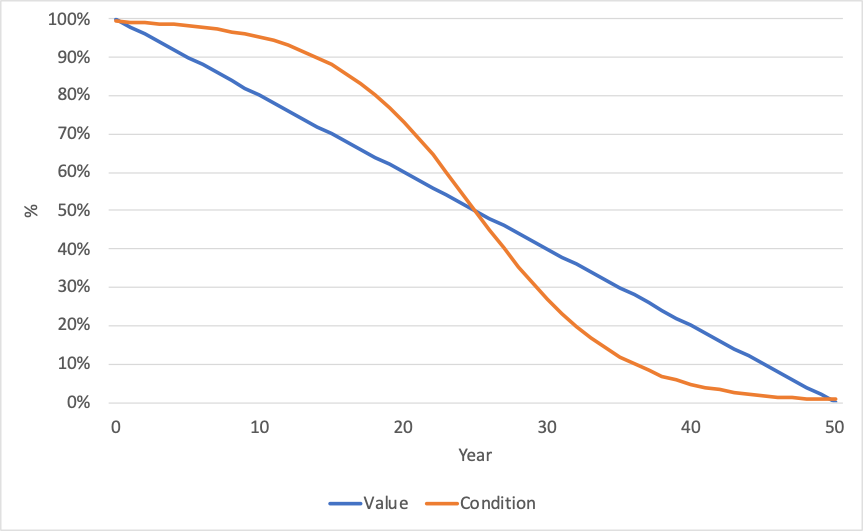
Depreciation may incorporate other factors beyond deterioration, as well. One key issue is technical obsolescence. Estimates of asset useful life typically incorporate assumptions concerning obsolescence, but this is not a factor incorporated into deterioration estimates. Assets can become obsolete due to technological or functional factors. For instance, a traffic controller may be in excellent physical condition, but would be considered to be obsolete if it no longer met industry technical standards and/or if it was no longer feasible to obtain replacement parts for the asset. Likewise, a bridge may be considered obsolete if designed to outdated functional standards for clearances and load carrying capacity. Typically once an asset is obsolete it assumed to be fully depreciated.
Another complicating factor that may be considered in calculating depreciation is the level of use of an asset, which may change either as a function of time, asset condition, or other factors. For example, a transit agency may use an older vehicle in poor condition less, utilizing newer, more reliable vehicles instead where feasible. On the other hand, for highway assets, traffic may continue to increase over time regardless of the condition of the asset, suggesting accelerating rather than decelerating depreciation.
Determining the various benefits an asset yields and how these vary over time can be an involved process. However, for most applications various simplifying assumptions are made to reduce the complexity. The different approaches can be grouped into three basic types, representing different levels of complexity in the calculations and data requirements. Table 6-1 lists the basic types of deprecation approaches and summarizes the strengths and weaknesses of each approach.
Table 6-1. Approaches for Calculating Depreciation
| Approach | Description | Strengths | Weaknesses |
|---|---|---|---|
| Actual Age | Depreciation increases linearly as a function of actual age | Straight-forward to calculate for new assets Requires few additional assumptions | Historic data may not be available, particularly for asset components Data on last treatment may be needed to establish age |
| Condition-Based | Depreciation increases linearly as a function of age adjusted for condition | Accommodates consideration of a wide range of treatments Can be calculated without historic data Supports evaluation of treatment selection and timing for TAM | Requires collecting condition data, frequently at a component level Can be a challenge to relate condition to remaining life, particularly for assets in very good or very poor condition |
| Non-Linear Benefit Consumption | Pattern of depreciation is determined based on a tailored analysis of how benefits are consumed | Flexible approach Consistent with U.S. and international accounting standards Best approach for matching actual pattern of use of an asset | Involves supplemental analysis Results may be dependent on parameters such as traffic growth and discount rate which are outside the control of an asset manager |
The simplest approach to calculating depreciation is to assume “straight-line depreciation” based on asset age. In this approach, one establishes the age of an asset or asset component, and then assumes depreciation increases in a linear fashion over the asset’s useful life. Thus, the value of the asset is presumed to decline by a constant value each year, dropping from the initial value to the end-of-life residual value. The virtue of this approach is its simplicity. When given an initial value, residual value, useful life, and asset age one can quickly determine asset value without any additional assumptions.
For any asset where very limited data exist, this relatively simple approach provides the asset manager with a functional method to determine a depreciation value. This approach can be applied to assets for which limited inventory data are available, assuming a distribution of asset age based on a model or sample data. Such approaches can be used to estimate value for assets such as signs and drainage structures which are numerous, but for which agencies may not have comprehensive data. Also, depreciating based on age can help address cases where an older asset becomes technically obsolete regardless of its physical condition.
In many cases, simply basing depreciation on an asset’s age can be too simple for supporting TAM applications. Often the age of an asset is a poor predictor of its remaining life, particularly if treatments have been performed to extend its life. Including effects of treatments further complicates the calculation. Replacing an asset resets its age, but what is the impact of a preservation action or a rehabilitation action? Further, many treatments impact one component of a complex asset but not others (e.g., the deck of a bridge but not the substructure; or the propulsion system of a rail car but not the carriage). Thus, when considering treatments short of replacement, one may need to track age and treatment effects at a component level.
A further complication is that it is frequently difficult to determine the age of an asset, particularly at a component level. We may know that a given section of a highway was constructed 40 years ago, but that does not necessarily imply that the pavement surface of the highway is 40 years old, let alone accompanying signs, guardrails, and other supporting assets.
Asset managers routinely contend with these challenges when modeling assets in their asset management systems. For some asset classes, such as guardrails and ITS, the asset’s age remains the best predictor of how the asset will perform and what treatments may be needed. Technical obsolescence can be a major factor for assets such as ITS devices. In some cases, there may be changes in standards or technical requirements that render assets obsolete sooner than would have been expected based upon their age. For complex assets, such as roads, bridges and facilities, information on asset age is supplemented with measurements of condition to better support TAM.
Where age data are unavailable or do not provide a reliable estimate of the remaining life of an asset, it may be preferable to base depreciation on an asset’s physical condition. If available, information on an asset’s condition can be used to obtain an improved estimate of the remaining life of an asset, and by extension, its effective age. There are many different approaches for utilizing condition data, but the approach that is recommended here can be generalized as follows: one obtains a revised, effective age for an asset using the available condition data, and then can proceed with asset valuation using this new effective age rather than actual asset age.
Note that the conversion of condition to age may involve a simple conversion and/or additional business rules. For instance, one may define a mapping of condition to percentage of life remaining, but decide to base the effective age on the actual age if the age or condition reach some threshold value. The key points are that condition is used in some manner to refine the estimate of an asset or asset component’s remaining life, and depreciation is assumed to proceed linearly once an age is established.
An alternative approach utilizing condition is to base depreciation strictly on condition without translating condition into an effective age. With this alternative approach it is implicitly assumed that benefits are consumed in proportion to the decline in condition, (which is typically a non-linear function). This approach is not recommended unless supported by additional analysis to verify the assumption that benefit consumption and condition change in direct proportion to one another. Where this alternative approach is used, it falls in the domain of a non-linear benefit consumption pattern as described further in the next section.
The basic advantage of calculating an effective age is that it leverages available condition data to provide a better estimate of how much of an asset’s value actually remains. Also, with this approach one can incorporate effects of treatments in the calculation of current value without specific knowledge of the treatment history of an asset. On the other hand, calculating effective age is practical only if condition data are actually available. Frequently, asset managers face limits to the available data, so in many cases, they rely on results of visual inspections and/or measurements of surface distresses. Needless to say, there are many challenges in relating the available data to the remaining service life of an asset.
With both of the general approaches described above, benefit consumption is assumed to be linear with respect to asset age (either actual or effective). A linear model should be assumed for depreciation unless there is evidence to suggest otherwise. This approach follows the maxim often attributed to Albert Einstein: “Everything should be made as simple as possible, but not simpler.”
However, in some cases an asset manager may have reason to believe that an asset will depreciate in some other manner. The final group of depreciation approaches encompasses the set for which benefits are consumed in a non-linear manner. When using a non-linear approach, one must carefully consider what benefits are being modeled and how these are actually consumed. Once a pattern is established, it can be mapped to actual or effective asset age to calculate depreciation.
Figure 6-2 provides an example illustrating the impact of different non-linear benefit consumption patterns. In both cases depreciation is shown as a percentage of an asset’s initial value with an assumed residual value of 0. Here the asset is assumed to have a useful life of 50 years.
In the case of the lower, concave curve depreciation is accelerated: the asset loses more of its value initially and less towards the end of its useful life. This curve was developed using an exponential function of the following form:
\begin{align*} D(t) &= (V(t_0) - RV) * (1 - (1 - r)^t) \end{align*}
where:
This pattern of depreciation is applicable if the use of an asset decreases as it ages, such as in the example of a revenue vehicle described above. It can be used to support certain traditional accounting approaches, including “declining balance depreciation” and “double declining balance depreciation” as described in by Dojutrek, et. al. (35). To use declining balance depreciation, one would set r to be equal to \frac{1}{N} where N is the useful life of the asset. To use double declining depreciation, one would set r to be \frac{2}{N}.
For the upper curve depreciation is decelerated: the asset loses less of its value initially, but then depreciation accelerates towards the end of the asset’s useful life. This curve was developed using a logistic function of the following form:
\begin{align*} D(t) &= \frac{V(t_0) - RV}{1 + e^{c_1 + c_2t}} \end{align*}
where c_1 and c_2 are constants.
This functional form may be applicable in cases where use of an asset is increasing over time, and/or where an asset’s benefits are proportional to asset condition. For instance, in the case of pavement, asset value may be represented using a condition index that is inversely proportional to road user costs.
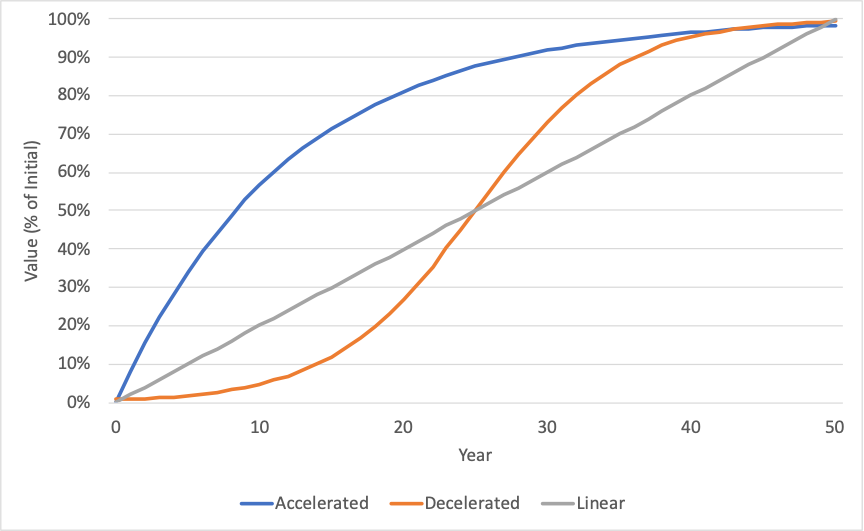
The approach of defining a customized, non-linear depreciation curve to match the pattern of consumption of an asset’s benefits is flexible, and consistent with U.S. and international accounting standards. Also, it is highly compatible with the economic perspective of asset value. If one has calculated initial asset value based on economic value, then establishing a specific pattern of depreciation can be performed using the same data compiled to calculate initial value.
The challenge with this approach is that it can be time consuming to perform the analysis required to establish an alternative benefit consumption pattern. Also, the results may hinge on assumptions outside the control of the asset manager, such as traffic growth. An asset manager may ask whether “the juice is worth the squeeze” before undertaking the additional analysis required for this approach.
While all of the approaches for calculating depreciation are valid, various approaches are preferable for certain TAM applications and depending on what data one has available. Figure 6-3 is a flowchart recommending an approach for calculating depreciation. Following the chart, results in a recommendation to either avoid the depreciation calculation entirely, depreciate linearly based on actual age, depreciate linearly using a condition-based approach, or perform supplemental analysis to establish the depreciation pattern if there is reason to believe it is non-linear. The basic logic reflected in the flowchart is:
- In certain cases, it is not necessary to calculate depreciation. If one is using the GASB 34 modified approach a cost to maintain is calculated using an organization’s management systems, but depreciation is not specifically calculated. In cases where one requires the current value of the asset and obtains this from the calculation of initial value – e.g., in the case of economic or market value – then additional calculation of depreciation is not needed. In all other cases, depreciation should be calculated.
- Linear depreciation based on actual age should be used as the basis for depreciation if this approach was used for financial reporting based on GASB 34 and the agency seeks to maintain consistency with its financial reporting. GASB 34 does not require that agencies assume linear depreciation based on asset age, but this is the approach that is almost invariably used except in cases where an agency uses the GASB 34 modified approach.
- Depreciation is important when using the replacement cost method because it indicates asset condition. Replacement cost alone only provides the “worst-case” estimate of asset cost. By accounting for depreciation, agencies demonstrate a commitment to maintaining the asset and avoiding the single, large replacement cost at the end of the asset’s life.
- In cases where depreciation is calculated and consistency with the approach used for financial reporting is not strictly required, then one must next ask whether there is reason to believe the pattern of benefit consumption may be non-linear. If this is the case, then further analysis will be required to establish the specific depreciation approach.
- Otherwise, one should use condition data to establish effective age if condition data are available and provide a meaningful estimate of the remaining life of an asset. Actual age should be used if condition data are unavailable, or if asset condition does not help predict remaining life (e.g., for assets that tend to be replaced due to obsolescence).
Note that based on the flow chart does there may arise a case where it is preferable to base depreciation on condition, but condition data are unavailable. In the flow chart one is directed to use an age-based approach in this case. However, this raises a broader question of what data an agency collects on its assets and how to assess data needs. NCHRP Report 956 (17), Chapter 7 of the AASHTO TAM Guide, Second Edition (5), and Chapter 8.5 of the AASHTO TAM Guide, First Edition (36) are all valuable references for further discussion of this topic.
This section describes the specific steps involved using the three different depreciation approaches addressed in this chapter: linear depreciation based on actual age (“age-based”); a linear-based depreciation using a condition-based approach (“condition-based”); and non-linear depreciation established through analysis of the pattern of benefit consumption (“non-linear”).
Note that the steps presented here describe the case in which depreciation is calculated for an individual asset or component since the point at which the initial value was calculated as described in Chapter 4, or since the last treatment, if a treatment was performed more recently than the time of the initial value calculation. However, depreciation can be calculated for other contexts using the same basic steps. For instance, one can use the steps described here to calculate the cumulative depreciation of an asset looking back in time prior to a recent valuation, predict future depreciation when testing different scenarios or treatment assumptions, or calculate depreciation for an inventory rather than an individual asset.
The steps for calculating depreciation using an age-based approach are described below. The steps describe the case where depreciation is calculated relative to the last treatment, or relative to the calculation of initial value described in Chapter 4 – whichever is later. If the only treatment being considered in the analysis is the construction or reconstruction of an asset, then depreciation is calculated since the asset was first purchased, constructed or reconstructed. If additional treatments are included, then depreciation is calculated from the time of asset purchase or construction until a treatment occurs. Overall asset value is a function of the initial asset value, value added through treatments, and value lost from depreciation. The overall calculation process is discussed further in Chapter 7.
Note that depreciation can never be greater than asset value, or an asset’s value would be deemed to be negative, and thus the asset would become a liability.
- Step 1 – Compile Data:
For each asset class and type of component being valued, compile the available data on the asset inventory and its age. Also compile the key parameters established through prior steps, such as useful life and residual value. If treatments other than asset purchase, construction/reconstruction are included, compile the available data on asset treatment history. The assumptions developed previously regarding the level of detail in the analysis and treatments to include may need to be revisited based on what data are available.
- Step 2 – Determine Asset Age:
Specify age at the level of detail established for the calculation – e.g., by individual asset or as a distribution of ages for the inventory. Refer to Chapter 13 of Measuring Capital (11) for guidance on estimating age distributions based on useful life if age data are unavailable.
- Step 3 – Calculate Depreciation:
Use the following equation to calculate depreciation D at time t:
\begin{align*} D(t) &= \frac{(V(t_0)-RV) * (A(t) - A(t_0))}{UL - A(t_0)} \end{align*}
where:
V(t_0) =value at time t_0;RV =residual value;UL =useful life;A(t) =asset age at time t;A(t_0) =asset age at time t_0;Note that when the initial value is based on current replacement cost and residual value is 0 this simplifies to the following:
\begin{align*} D(t) &= \frac{Replacement Cost * A(t)}{UL} \end{align*}
Generally the steps followed using a condition-based approach are similar to those described above for an age-based approach, with two important differences. That is, the determination of asset age is more involved in this case. The condition may be used as the sole determinant of effective age, or as a factor that modifies the effective age. Further, in the event that effective age is based strictly upon an asset’s condition then historic asset data is technically not needed in this case (though presumably would be used to established technical parameters such as unit costs and useful lives).
- Step 1 – Map Asset Condition to Effective Age:
For each asset class and type of component being valued, determine how asset condition relates to age. If condition is the best predictor of remaining life, then a simple function or lookup table can be defined to predict effective age for each feasible condition value. Alternatively, one may predict effective age based on condition, actual age and/or other variables. Refer to NCHRP Report 713 (18) for detailed guidance on modeling asset life.
- Step 2 – Compile Data:
For each asset class and type of component being valued, compile the available data on the asset inventory and its condition. If the calculation of effective age requires knowledge of actual age, also compile data on asset age and prior treatments that impact age. Also compile the key parameters established through prior steps, such as useful life and residual value. The assumptions developed previously regarding the level of detail in the analysis and treatments to include may need to be revisited based on what data are available.
- Step 3 – Determine Asset Age:
Specify effective age at the level of detail established for the calculation using the approach established in Step 1.
- Step 4 – Calculate Depreciation:
Use the following equation to calculate depreciation D at time t:
\begin{align*} D(t) &= \frac{(V(t_0)-RV) * (E(t) - E(t_0))}{UL - E(t_0)} \end{align*}
where:
V(t_0) =value at time t_0;RV =residual value;UL =useful life;E(t) =asset age at time t;E(t_0) =asset age at time t_0;Note that when the initial value is based on current replacement cost and residual value is 0 this simplifies to the following:
\begin{align*} D(t) &= \frac{Replacement Cost * E(t)}{UL} \end{align*}
The final option for calculating depreciation is the most complicated of the three. With this approach, one must understand how the benefits of an asset are actually being consumed over time, and structure the depreciation function accordingly.
For this approach it is necessary to define what the benefits of an asset are, and then establish a function for predicting how these benefits are consumed. Factors to consider in establishing asset benefits are:
- Level of use – traffic volume or ridership patterns over time. As described above, for highway assets often traffic is assumed to increase over time, which tends to result in accelerating depreciation. On the other hand, if an asset is utilized less as it ages then depreciation may decelerate over time.
- Travel time, operating and social costs – generally the benefit of a transportation asset is that it supports mobility. Thus, in many cases the basic benefit an asset provides can be measured in terms of the savings in travel time, operating and social costs experienced if the asset is in service in good condition relative to the case where the asset is allowed to deteriorate. For instance, as a road deteriorates its surface roughness increases, potentially increasing traffic congestion – and thus user travel time and social costs of transportation – and increasing vehicle operating costs.
- Asset failure – as an asset deteriorates it is more likely that the asset will fail in some manner, requiring emergency repairs, as well as temporary or complete closure. Where the likelihood of asset failure can be related to asset condition these costs tend to increase over time.
Once the benefits of an asset are established, it is necessary to define a function for representing how benefits are consumed over time. There is no single functional form that can be used for this step, though exponential and logistic curves provide flexibility for capturing a range of different depreciation patterns. A common approach is to use “declining balance depreciation,” in which an asset loses a specified percentage each year. Various other approaches have been defined in the accounting literature, most of which result in accelerated depreciation early in an asset’s life, such as double declining balance and sum of year’s digit’s appreciation. The following steps describe a basic approach to establishing the depreciation relationship considering a non-linear depreciation pattern.
- Step 1 – Quantify Asset Benefits:
For each asset class and type of component being valued, establish what benefits the asset yields, and how these vary over the life of an asset. Consider agency, user and social costs and benefits, and how these vary over time, as well as based on an asset’s condition.
- Step 2 – Establish the Depreciation Curve:
Determine the functional form of the depreciation curve based on the results of Step 1. If the pattern of benefit consumption can be approximated using a linear relationship, then revert to using a linear model. Otherwise, determine whether the depreciation pattern is accelerated or decelerated relative to linear depreciation.
If the depreciation pattern is accelerated, evaluate whether a fixed depreciation rate can be used, resulting in use of an exponential curve as described in Section 6.1. If the depreciation pattern is decelerated related to linear depreciation, evaluate whether a logistic (s-shaped) curve can be used as described in Section 6.1. Otherwise develop a customized depreciation function.
- Step 3 – Compile Data:
For each asset class and type of component being valued, compile the available data on the asset inventory and other data required to support the depreciation calculation approach defined in Step 2. The assumptions developed previously regarding the level of detail in the analysis and treatments to include may need to be revisited based on what data are available.
- Step 4 – Calculate Depreciation:
Calculate depreciation using the relationship determined in Step 2 with the data compiled in Step 3.
The following are hypothetical examples illustrating the different depreciation approaches described in Section 6.2.
An agency has a bridge, initially constructed in 1960 with an expected lifespan of 70 years. In 2010, the asset was reconstructed and brought back to “like new” condition, resetting the its age to zero in 2010. The replacement cost of the bridge, in today’s dollars, is $5 million with a residual value of $1 million. The depreciation in year 2021 is calculated using the following formula from section 6.2.1:
\begin{align*} D(t) &= \frac{(V(t_0)-RV) * (A(t) - A(t_0))}{UL - A(t_0)} \newline D(t) &= \frac{(5,000,000 - 1,000,000) * (11 - 0)}{(70 - 0)} \newline D(t) &= 628,570 \end{align*}
where:
The new value of the asset is $4.37 million.
This example illustrates that how an age-based approach can be utilized in cases where a treatment has the effect of resetting the age. It is more challenging to apply this approach to a case where a rehabilitation is performed that improves the condition of the asset but does not restore it to “like new” condition.
An agency has installed a set of 100 fareboxes on its buses. Each farebox cost approximately $5,000 in current dollars to install. The agency maintains maintenance records on its fareboxes documenting their condition. However, the agency decides to calculate depreciation based on age given fareboxes typically are replaced on a 15-year cycle as a result of technical obsolescence rather than deteriorated condition.
Based on these assumptions the agency determines that a farebox depreciates by $5,000/15 = $333.33 per year until it reaches 15 years. The table below shows a set of example calculations assuming fareboxes of varying age. Based on the table, the initial value of the 100 fareboxes is $500,000. Depreciation totals $265,000, resulting in a current value of $235,000.
Table 6-2. Example Calculation of Asset Value for an Inventory of Fareboxes
| Age (years) | Count | Initial Value ($) | Depreciation ($) | Current Value ($) |
|---|---|---|---|---|
| 0 | 5 | 25,000 | 0 | 25,000 |
| 1 | 6 | 30,000 | 2,000 | 28,000 |
| 2 | 5 | 25,000 | 3,333 | 21,667 |
| 3 | 4 | 20,000 | 4,000 | 16,000 |
| 4 | 3 | 15,000 | 4,000 | 11,000 |
| 5 | 0 | 0 | 0 | 0 |
| 6 | 11 | 55,000 | 22,000 | 33,000 |
| 7 | 10 | 50,000 | 23,333 | 26,667 |
| 8 | 13 | 65,000 | 34,667 | 30,333 |
| 9 | 9 | 45,000 | 27,000 | 18,000 |
| 10 | 5 | 25,000 | 16,667 | 8,333 |
| 11 | 4 | 20,000 | 14,667 | 5,333 |
| 12 | 7 | 35,000 | 28,000 | 7,000 |
| 13 | 4 | 20,000 | 17,333 | 2,667 |
| 14 | 6 | 30,000 | 28,000 | 2,000 |
| >15 | 8 | 40,000 | 40,000 | 0 |
| Total | 100 | 500,000 | 265,000 | 235,000 |
The Kentucky Transportation Cabinet (KYTC) uses a condition-based depreciation approach for valuing assets in its TAMP (37). For bridges KYTC bases depreciation on the NBI condition ratings for the deck, superstructure, and substructure of each bridge. For each value in the NBI scale KYTC has established an equivalent percent of depreciated value, as shown in Figure 6-4.
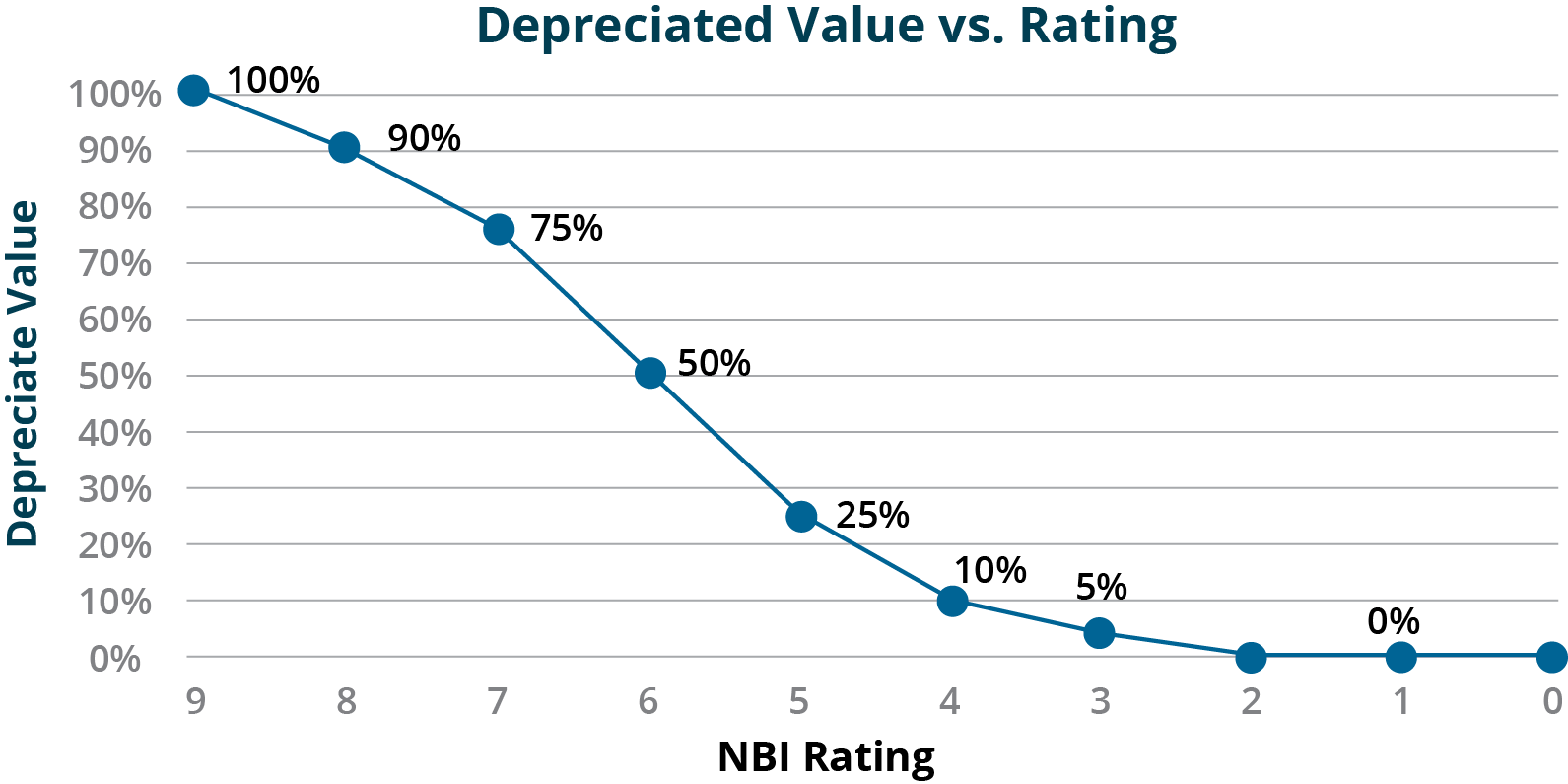
In Table 6-2 this depreciated value is mapped to an effective remaining service life using KYTC’s assumed useful life of 75 years for a new bridge. The remaining asset life can be substituted into the equation shown in Example 6-1 to calculate depreciation in dollars as a function of condition. The table shows an example of the calculations for a component with an initial value of $10 million.
Table 6-3. Effective Remaining Life and Depreciation Calculations by Condition Rating
| Condition Rating | Depreciated Value (see Figure 6-4) | Effective Remaining Useful Life (years) | Depreciation Given Initial Value of $10M ($M) | Current Value Given Initial Value of $10M ($M) |
|---|---|---|---|---|
| 9 | 100% | 75.00 | 0.0 | 10.0 |
| 8 | 90% | 67.50 | 1.0 | 9.0 |
| 7 | 75% | 56.25 | 2.5 | 7.5 |
| 6 | 50% | 37.50 | 5.0 | 5.0 |
| 5 | 25% | 18.75 | 7.5 | 2.5 |
| 4 | 10% | 7.50 | 9.0 | 1.0 |
| 3 | 5% | 3.75 | 9.5 | 0.5 |
| 2 | 0% | 0.00 | 10.0 | 0.0 |
| 1 | 0% | 0.00 | 10.0 | 0.0 |
A highway agency is interested in analyzing the pattern of consumption of benefits for pavement. Pavement management staff model the benefit of a pavement section as providing mobility for road users, reducing travel time and operating costs relative to an alternative of using other roads in the event the pavement section was out of service. Over time the use of the pavement increases, in theory yielding greater benefits. However, as the pavement ages roughness increases, reducing benefits obtained from the pavement.
To model these effects the agency staff utilize the model of pavement user costs detailed in NCHRP Report 866 (38). Using the model provided with this report they predict the excess user costs for different representative pavement sections. Figure 6-5 shows the excess user cost as a function of IRI for a 1-mile urban principal arterial with daily traffic of 1,000 vehicles calculated using this model.
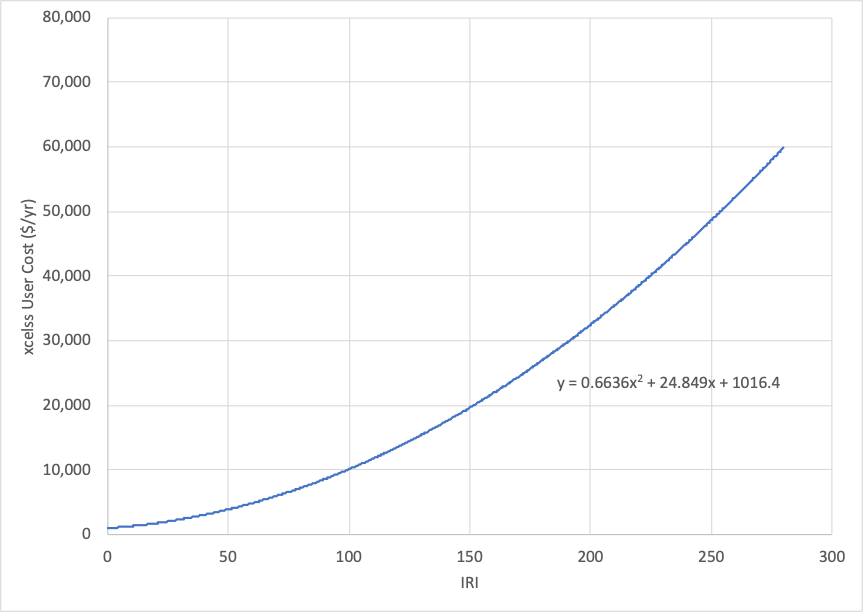
The staff use relationships obtained using the NCHRP report to estimate the benefits realized from a pavement section over time. This is then used to estimate the depreciation curve for pavement. Figure 6-6 shows an example curve for a one-mile section with 1,000 daily vehicles, assuming 5% annual growth in traffic.
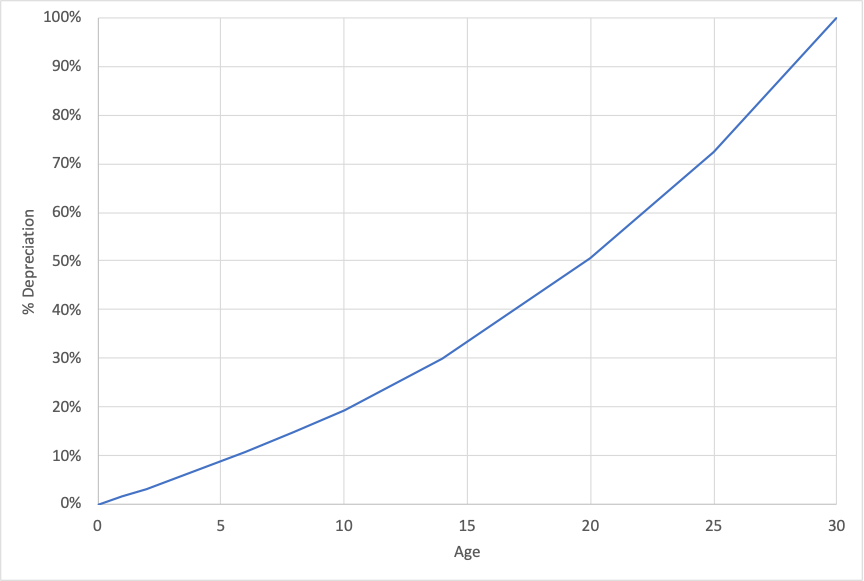
This section provides examples of “emerging,” “strengthening,” and “advanced” practices with respect to calculation of depreciation. Maturity levels are defined for each of the for two basic cases described in the guidance, that one has age data, or that one has condition data. In both cases there is an additional option to assume a linear pattern of depreciation with respect to age/effective age, or to perform a supplemental analysis to analyze the pattern of benefit consumption for the asset. In the table an emerging practice is one that supports the guidance with minimal complexity, an advanced practice illustrates a “state of the art” example in which an agency has addressed some aspect of the asset value calculation in a comprehensive manner, and strengthening practice lies between these two levels.
Asset age is not well established. Costs by asset class are calculated by year and depreciated without associating costs to specific assets.
Asset or component age is known or can be estimated based on inventory and treatment data, supporting calculation of depreciation at an asset class, asset and/or component level.
Asset age or component age is known or can be estimated based on inventory and treatment data. An analysis is performed of the consumption of asset benefits. A custom pattern of benefit consumption is used if supported by the analysis. Depreciation is calculated based on the selected approach by asset class, asset and/or component.
Condition data are sufficient for estimating the condition distribution at a network level. Condition is mapped to effective age and depreciation is calculated by asset class based on current condition.
An assessment is performed to determine how best to calculate effective age, potentially using actual age and/or condition. Depreciation is calculated based on effective age by asset class, asset and/or component.
An analysis is performed of the consumption of asset benefits. A custom pattern of benefit consumption is used if supported by the analysis. Otherwise, an assessment is performed to determine how best to calculate effective age, potentially using actual age and/or condition. Depreciation is calculated based on the selected approach by asset class, asset and/or component.
The discussion of how to calculate asset value has thus far focused on how to perform the calculation for a single asset or asset component. This section addresses the question of how to perform the calculation for groups of assets. The following subsections provide an overview of the calculation process and key issues, and recommended calculation steps.
The steps detailed in Chapter 3 to 6 detail all of the building blocks of the asset value calculation. The only remaining step to calculate the value of a given asset or component at time t is to subtract depreciation from the initial asset value :
\begin{equation*} V(t) = V(t_0) - D(t) \end{equation*}
In practice, however, the calculation does not stop there. For most applications one seeks to calculate the value for multiple assets and asset classes, requiring some form of aggregation. Also, one should ideally account for the fact that there is inherent uncertainty in the calculations of asset value, particularly if they are prospective (predictions of future value) rather than retrospective. Additional analysis may be required to address these and other issues.
Note that depreciation should never exceed the initial value of the asset or component. This and other calculation issues may arise depending on the level of detail at which calculations are performed, determination of how different treatments are incorporated in the calculations, and approach used for componentization (discussed in Chapter 3).
Asset Aggregation
Aggregating asset value calculations can be accomplished in two basic ways: either the asset value calculation is performed for individual assets or components and then the results are aggregated, or assets are grouped together for analysis first and the calculation of value is performed at an aggregate level.
Performing calculations on aggregated data is preferable, as doing so saves effort. However, it is important not to introduce errors in the calculation process by over-aggregating. When data are aggregated one relies on averaging to obtain an aggregate result. Provided the groups of assets are homogenous in their characteristics and all of the underlying relationships being modeled are linear, then one can aggregate prior to calculating value. However, if there is a lack of homogeneity or non-linear effects then aggregating can introduce errors. Examples of situations where aggregation may not be appropriate include:
- Initial costs are calculated using a more complex method than a simple unit cost;
- Initial costs are calculated using a simple unit cost, but this unit costs varies for different assets in the group;
- Useful lives vary for different assets in the group;
- Depreciation is non-linear;
- An asset consists of multiple components with different ages and useful lives, but is being valued at the asset level rather than component level; and/or
- One or more assets or components are fully depreciated.
Table 7-1 illustrates the issue. Here value is calculated using age-based depreciation for assets A and B. The calculation is performed separately for both, and then at an aggregate level combining the two assets. The table shows the initial value of each asset, and the accumulated depreciation. It also shows the current value, which is the initial value less depreciation. When the calculation is performed separately for each asset the total current value is calculated as $8.2 million. However, when A and B are treated as a single asset, the value calculated is $4.2 million – substantially less!
The culprit responsible for the error in this case is the treatment of depreciation. Asset B is older than the useful life of 50 years, and thus fully depreciated. Once an asset is fully depreciated its value is assumed to be equal to its residual value and not allowed to become negative. This effect is correctly accounted for when the calculations are performed by asset, but ignored in the aggregate calculation in which the average age is used.
Table 7-1. Approaches for Calculating Depreciation
| Measure | A | B | Total if Calculated by Asset | Total if Assets are Aggregated |
|---|---|---|---|---|
| Initial Value ($ million) | 11.0 | 22.0 | 33.0 | 33.0 |
| Residual Value | 1.0 | 2.0 | 3.0 | 3.0 |
| Age (years) | 24 | 60 | N/A | 48 |
| Useful Life (years) | 50 | 50 | N/A | 50 |
| Depreciation ($ million) | 4.8 | 20.0 | 24.8 | 28.8 |
| Current Value ($ million) | 6.2 | 2.0 | 8.2 | 4.2 |
Ultimately, establishing the correct level of aggregation requires careful consideration of the approach and experienced judgement to determine the appropriate level of detail based on the approach and the asset characteristics.
Treatment of Uncertainty
The quantitative approaches described in this guide are deterministic – they assume that calculation parameters are known with certainty. In reality key parameters are subject to uncertainty and error, particularly when an analysis is performed at an aggregate level. For example:
- Treatment costs and effects can be highly variable and depending on a large number of factors.
- Future asset deterioration is uncertain, and subject to changes as a result of changing technology, the changing climate, and myriad other factors.
- Future traffic/level of use will drive the benefits obtained from an asset and also depend on economic and demographic factors well outside of the control of an asset manager.
- Economic parameters such as inflation, the discount rate, and the value of time are subject to uncertainty and may be computed differently depending on one’s assumptions.
In certain respects, calculating asset value at an aggregate level can help address some of the inherent uncertainties underlying the calculations given parameters such as treatment costs and treatment effects are often derived at this level. Asset level calculations may be more precise – but no more accurate – if they rely on highly variable parameters derived through observations of large populations of assets.
A number of approaches have been developed for handling uncertainty in numeric calculations. Uncertainty is inevitable in calculations of asset value; the question for the analyst is whether the level of uncertainty is tolerable given the manner in which the results of the calculation will be used. The approach recommended here is to acknowledge where uncertainty exists, and – if sufficient time and resources are available – perform sensitivity analyses to show the degree to which changes in key parameters would impact the results of the analysis. For calculations of current value, the analysis may, at a minimum, include testing the impact of changes in asset useful life. For predictions of future value an accompanying sensitivity analysis should also address changes in treatment costs and any economic parameters used in the calculation approach (e.g., the discount rate, if applicable).
The following steps are recommended for calculating current asset value for one or more asset classes and components. These build on the results of prior steps for establishing the scope of the analysis, selecting the initial value calculation approach, identifying treatments, and selecting the depreciation approach.
- Step 1 – Review the Level of Detail in the Calculations:
Review the decisions made on the level of detail in the asset value calculation made in Step 1. Combine assets to perform a more aggregated analysis if feasible without significantly impacting the results. Disaggregate the analysis further if key parameters such as costs and useful lives are found to vary within subgroups of assets.
- Step 2 – Calculate Initial Value:
Apply the approach selected previously to calculate initial value for each asset group, asset or component. Note that in cases where treatments besides initial purchase/construction are included in the analysis and depreciation is based in part or entirely on age, the initial value should be calculated as of the time of the most recent treatment. (but may not be the same as that of a “like new” asset unless the most recent treatment was replacement or reconstruction).
- Step 3 – Calculate Depreciation:
Apply the selected approach to calculate depreciation for each asset group, asset or component.
- Step 4 – Calculate Asset Value:
Calculate value as the difference between initial value and accumulated depreciation. Sum the results across components, assets and/or asset classes to obtain total asset value.
- Step 5 – Conduct Sensitivity Analysis:
Document the impact of changes to key parameters on the calculations of asset value.
Asset value is an important component in an organization’s financial reports. Much of the prior guidance for calculating asset value has focused on this application. While this guide concentrates on the calculation of asset value to support TAM rather than financial reporting, an asset manager should remain mindful of how an agency develops its financial reports, how asset value is calculated in these reports, and any differences between TAM and financial reporting approaches. The following subsections summarize U.S. public agency financial reporting requirements, and discuss discrepancies between approaches used for asset valuation in financial reporting and TAM.
Financial reporting requirements for U.S. public agencies are detailed in GASB Statement 34 (1). This document requires public agencies to prepare basic financial statements. These should include:
- Assets, distinguishing between capital and other assets
- Liabilities, distinguishing between long-term liabilities and other liabilities
- Net assets, distinguishing among amounts invested in capital assets, net of related debt; restricted amounts; and unrestricted amounts
- Revenues by major source
- Expenses
- Excess or deficiency before contributions
- Contributions
- Special and extraordinary items
- Transfers
- Change in net assets
- Ending net assets
Capital assets are included in the calculation of net assets, but are often presented in a separate table in the financial report. These are defined to include “land, improvements to land, easements, buildings, building improvements, vehicles, machinery, equipment, works of art and historical treasures, infrastructure, and all other tangible or intangible assets that are used in operations and that have initial useful lives extending beyond a single reporting period.” Infrastructure assets are further defined as “long-lived capital assets that normally are stationary in nature and normally can be preserved for a significantly greater number of years than most capital assets.” GASB 34 cites as examples of infrastructure assets roads, bridges, tunnels, drainage systems, water and sewer systems, dams and lighting systems.
GASB 34 requires that capital assets are valued using historic costs. Capital assets should be depreciated, but if an agency elects to use the “modified approach” described in Chapter 2 for its infrastructure assets, it is not required that these are depreciated. Instead, the cost to maintain these assets at a specified level of service is established and expensed within the year the cost is incurred.
Tables 7-2 and 7-3 provide examples showing how capital assets are presented in public agency financial reports. Table 7-2 is an excerpt from the Oregon DOT financial statement (39). It shows the beginning balance, increase, decrease and ending balance for each type of capital asset. The value of the state highway and bridge system is reported as a single item in the table with a beginning balance of approximately $14.5 billion and an ending balance of approximately $14.8 billion. In this case, the agency depreciates the value of the system, showing a decrease of $69.7 million from annual depreciation.
Table 7-2. Example Statement of Capital Asset Activity – Oregon DOT - Source Oregon DOT (39)
| Beginning Balance | Increases | Decreases | Ending Balance | |
|---|---|---|---|---|
| Buildings | $ 282,559,529 | $ 5,825,276 | $ (1,011,511) | $ 287,373,294 |
| Construction in progress - infrastructure | $ 523,786,457 | $ 350,031,308 | $ (253,454,458) | $ 620,363,307 |
| Construction in progress - other | $ 26,461,827 | $ 17,021,568 | $ (18,255,339) | $ 25,228,056 |
| Data processing software | $ 106,812,614 | $ 24,478,495 | $ (1,059,400) | $ 130,231,709 |
| Land | $ 1,710,428,334 | $ 12,918,983 | $ (1,570,400) | $ 1,721,776,917 |
| Land improvements | $ 192,994,657 | $ 2,577,734 | $ (286,774) | $ 195,285,617 |
| Land use rights (amortized) | $ 781,932 | - | - | $ 781,932 |
| Leasehold improvements | $ 3,999,333 | $ 13,500 | - | $ 4,012,833 |
| Machinery and equipment | $ 444,479,092 | $ 18,807,518 | $ (25,186,989) | $ 438,099,621 |
| State highway and bridge system | $ 14,465,090,764 | $ 379,248,721 | $ (69,746,542) | $ 14,774,592,943 |
| Works of art and historical treasures | $ 101,151 | - | - | $ 101,151 |
| Total capital assets | $ 17,757,495,690 | $ 810,923,103 | $ (370,571,413) | $ 18,197,847,380 |
Table 7-3 is an excerpt from Michigan DOT showing how this agency reports changes in capital assets (40). Here roads and bridges are reported separately. They are included in the category of “Capital assets, not depreciated” as Michigan DOT uses the GASB 34 modified approach.
Table 7-3. Example Statement of Capital Asset Activity – Michigan DOT - Source: Michigan DOT (40)
| Beginning Balance | Additions | Deletions | Ending Balance | |
|---|---|---|---|---|
| Capital assets, not depreciated: | ||||
| Roads | $ 12,860.9 | $ 123.1 | $ (922.4) | $ 12,061.6 |
| Land | $ 3,146.5 | $ 7.8 | - | $ 3,154.3 |
| Bridges | $ 2,693.9 | $ 266.1 | $ (34.4) | $ 2,925.6 |
| Construction in progress | $ 1,744.4 | $ 1,002.5 | $ (472.3) | $ 2,274.7 |
| Computer software projects in progress | $ 6.8 | $ 2.4 | $ (6.8) | $ 2.4 |
| Land rights | $ 0.4 | $ 0.2 | - | $ 0.6 |
| Capital assets, depreciated: | ||||
| Equipment | $ 241.2 | $ 9.6 | $ (3.4) | $ 247.4 |
| Buildings | $ 168.9 | $ 5.4 | $ (0.1) | $ 174.1 |
| Blue water Bridge infrastructure | $ 32.1 | $ 3.5 | - | $ 35.6 |
| Railroads | $ 173.7 | - | - | $ 173.7 |
| Rest areas & welcome centers | $ 120.9 | - | - | $ 120.9 |
| Land improvements | $ 54.5 | $ 2.0 | $ (0.6) | $ 55.9 |
| Airports | $ 1.8 | - | - | $ 1.8 |
| Computer software | - | $ 6.8 | - | $ 6.8 |
| Less accumulated depreciation for: | ||||
| Equipment | $ (106.9) | $ (11.5) | $ 2.7 | $ (115.6) |
| Buildings | $ (88.0) | $ (7.1) | $ 0.1 | $ (95.1) |
| Blue water bridge infrastructure | $ (14.2) | $ (1.4) | - | $ (15.6) |
| Railroad | $ (54.6) | $ (4.1) | - | $ (58.7) |
| Rest area and welcome center | $ (51.9) | $ (2.7) | - | $ (54.6) |
| Land improvements | $ (14.1) | $ (2.7) | $ 0.3 | $ (16.4) |
| Airports | $ (1.0) | $ (0.1) | - | $ (1.1) |
| Computer software project | - | $ (1.1) | - | $ (1.1) |
| Total capital assets | $ 20,915.3 | $ 1,398.7 | $ (1,436.7) | $ 20,877.2 |
The Oregon and Michigan examples are typical of other public agency financial reports. These examples are prepared in a manner that complies with GASB requirements. Asset value is consistently reported for transportation assets using historic costs. Annual depreciation is presented where the agency does not use the modified approach, and agency expenses on infrastructure assets are reported in lieu of depreciation where the modified approach is used. However, the presentation is relatively compact and omits many details that may be of value for asset management purposes, such as details on value by system (e.g., Interstates, NHS) or asset subclass.
As discussed in Chapter 2, the use of historic costs, while consistent with best practices in accounting, limits the use of the financial report values for other purposes. However, the GASB 34 modified approach yields an estimate of the cost to maintain the transportation system which is valuable for supporting TAM. Thus, in the event an agency uses the GASB 34 modified approach for financial reporting, an option for supporting TAM is to utilize a consistent approach for reporting asset value in TAM documents, emphasizing the use of the cost to maintain rather than attempting to derive a separate calculation of depreciation. The NHS portion of the overall cost to maintain, calculated using the modified approach, is equivalent to the cost to maintain current value required for NHS TAMPs prepared by State DOTs.
Where the GASB 34 modified approach is not used, it may be preferable to calculate asset value based on replacement cost or market value rather than historic cost. In this case the asset value calculated for TAM inevitably differs from that reported in an agency’s financial report. The following approach is recommended to resolve the discrepancy between asset value reported in financial report and TAM documents:
- When calculating asset value for TAM applications, asset managers should carefully review the calculation of asset value in the agency’s financial report and obtain further detail on the value by system or asset subclass where possible. It is important to establish “line of sight” between the inventory data used for TAM and that used for financial reporting data (see sidebar).
- To the extent feasible, different calculations of asset value should use common assumptions regarding key parameters, such as replacement costs and asset lives.
- Where it is not feasible to use common assumptions, the differences between approaches should be well documented. Over time it may be feasible to resolve the differences in approaches either by revising the asset valuation approach or presenting additional information in the agency’s documents to clarify the different calculations of asset value.
Often there are discrepancies between the asset register used for financial reporting and the asset hierarchy and inventory data used for TAM. Ideally an agency should resolve these discrepancies, so there is a clear “line of sight”.
This section discusses how to calculate a set of performance measures related to asset value: the cost to maintain current value, asset consumption ratio, asset sustainability ratio, asset renewal funding ratio, and net present value. For each a definition of the measure is provided, along with guidance for calculating the measure and a discussion of the measure’s strengths and limitations.
Note the definitions presented in this guide are similar to those presented in other related guidance, most notably the Institute of Public Works Engineering Australasia (IPWEA) Australian Infrastructure Financial Management Manual (AIFMM) (9). However, these have been adapted and revised for U.S. agency use and to reflect the range of different valuation approaches presented here.
The cost to maintain current asset value helps answer an important question any asset owner is inclined to ask: “how much money do we need to spend?” FHWA requires that State DOTs quantify this value for their NHS roads and bridges in their NHS TAMP. The definition of this measure is shown in the call-out box.
Average annual asset preservation, rehabilitation and replacement funding which, if spent over a specified period, is predicted to result in an ending asset value equal to the value at the start of the period.
One can approximate the cost to maintain current value by determining annual depreciation for a system. If an agency spent this amount on its system in a given year, then all things being equal, the new spending would offset the annual depreciation, with the result that current value maintained.
However, while this approach to calculating the measure is quite tidy, it suffers from being potentially inaccurate. For complex assets the treatment requirements and costs required for an asset – and to maintain service while the asset is being treated – may bear little resemblance to the cost of constructing a new asset used in the asset value calculation. Also, in many cases the asset value calculation excludes the cost of treatments that impact asset condition. Further, when one bases the estimate on annual depreciation, this provides little basis for further detailing how the cost, if spent, would actually need to be distributed between different assets or treatments.
To address these issues, an agency should ideally calculate the cost to maintain asset value by utilizing its asset management systems. With this approach, asset managers define different potential investment scenarios and identify the least expensive scenario that will maintain or improve average asset conditions and asset value. The reported cost should include all of the costs modeled in the agency’s management system used to determine the cost to maintain, which may include other treatments not modeled in the agency’s calculation of asset value.
One challenge in using this measure is that the cost to maintain assets’ current conditions may be very different from that which an agency needs to spend to maintain its assets in their desired state of good repair. For very new assets, it is inevitable that the asset inventory will initially decline in condition somewhat. For a deteriorated system, it may be necessary to maintain and improve conditions and value.
The Asset Sustainability Ratio (ASR) is the ratio of annual asset expenditures to the cost to maintain current value. If the ratio is 1, then annual expenditures are sufficient for maintaining value. If the ratio is less than 1 the system is likely to lose value, and if it is greater than 1 the system is likely to gain value.
The ratio of annual asset expenditures, omitting improvements, to the cost to maintain current value. All types of expenditures included in the cost to maintain current value should be included in the calculation of asset expenditures.
The measure has been in use in Australian financial reporting since the early 2000’s as described by the Local Government Association of South Australia (LGASA) (41). Also, it is included as one of the key measures in the AIFMM (9).
ASR is a valuable measure for summarizing trends in asset spending. Like the cost to maintain current value, it helps identify areas where more spending is needed. Also, given it is a somewhat standardized measure, one can use it to compare asset maintenance methods and asset condition across different systems, assets and agencies.
In using ASR it is important to be clear about which costs are included in the calculation of current expenditures and the cost to maintain current value. The Australian definition relies on data available in a financial report: it is the renewal cost divided by annual depreciation. Here it is recommended that all expenditures included in the cost to maintain current value be included in the calculation, though some applications narrow the definition to include only asset renewals, or widen it to include all asset-related work. Further, here it is recommended that the cost to maintain current value be used in the denominator. This may or may not be equal to annual depreciation, depending on the approach used.
The basic challenge in interpreting ASR is the same as that described for the cost to maintain current value. That is, while it is generally desirable to maintain value, there may be cases where some loss of value is acceptable (implying ASR should be less than 1) or where value needs to be increased (implying ASR should be greater than 1). For example a new asset would be expected to lose value initially even if well maintained. Conversely, if a system is in a poor state of repair, then simply maintaining current conditions may not be desirable.
The Asset Consumption Ratio (ACR) quantifies the portion of the asset that remains after accounting for depreciation. That is, it indicates what percentage of an asset remains to be consumed. This measure ranges from 0 for an asset that is fully depreciated (completely consumed) to 1 (100%) for a new asset. Like ASR, ACR has been used in Australian financial reporting since the early 2000’s (41).
The ratio of current asset value to the initial value of an asset when purchased or constructed.
Note this measure is meaningful only in cases where current replacement cost is used as the basis for measuring value, and where some form of depreciation is calculated.
ACR is valuable as a means for summarizing the relative condition of the asset inventory. It can be a valuable measure for helping summarize trends over time and/or for comparing different asset classes that are otherwise measured using different quantities and scales. However, some asset managers may find it superfluous if they already have well-established approaches for quantifying asset condition.
A challenge in interpreting ACR is in determining what is meant if the ACR is 0 for an asset. Does this mean the asset has failed or still operating but in need of replacement given it has reached its economic useful life and/or is now obsolete? Presentations of ACR should be supplemented with supporting details concerning the assumed useful lives and how these were derived.
The Asset Funding Ratio (AFR) is measure of whether an agency’s planned investments are sufficient for achieving and maintaining the agency’s desired state of good repair over a 10-year period. If this measure is 1 then planned expenditures are equal to the expenditures needed to achieve and maintain the desired state of good repair. If AFR is less than 1, then planned expenditures are insufficient, and it is likely that the desired state of good repair will not be maintained. A 10-year horizon is recommended to provide a comprehensive view of how an agency’s assets are performing over time.
The ratio of asset preservation, rehabilitation and replacement funding planned over a 10-year period to the total funding required over the same period to achieve and maintain the agency’s desired state of good repair.
AFR differs from ASR in what value is used for the denominator of the calculation: funding needed to achieve and maintain the desired state of good repair rather than the cost to maintain current value. In the case that the desired state of good repair is to maintain current conditions, AFR and ASR measure the same thing. However, in other cases AFR better accounts for situations described above that ASR does not address, where the desired condition of the asset inventory is different from current conditions. Note that AFR, as defined, is similar to the Asset Renewal Funding Ratio defined in the AIFMM (9) and the Asset Sustainability Index as defined by FHWA (42).
The challenge in using AFR is that it requires an organization to define its “desired state of good repair.” FHWA requires that State DOTs quantify this state for their NHS roads and bridges in their NHS TAMP. Also, agencies using the GASB 34 modified approach must define a similar concept, the target level of service for their infrastructure assets. However, it can be difficult to define this desired state or target level of service. Even if it is well defined, it may be difficult to make comparisons between different agencies using the measure, as they are likely to define their desired state differently. Thus, AFR is a valuable measure for showing whether a given agency is achieving its goals, but of more limited value for making comparisons over time or between agencies.
The final measure of interest related to asset value is Net Present Value (NPV). This measure is defined in Chapter 4 as the difference between total discounted benefits of an asset and total discounted costs. When economic value is used as the basis for calculating asset value then the resulting value of an asset is its NPV. If the NPV is positive then the asset or investment is considered worthy of investment. If the NPV is negative then the converse is true, and the cost of the asset is greater than the benefits it is expected to yield to society.
The difference between total discounted benefits and total discounted costs of an asset or investment.
Where some other basis is used for calculating value, the resulting asset value is analogous to NPV, but cannot be considered to be the same. However, one can still use asset value to support the calculation of NPV when comparing two potential life cycle alternatives. Asset value can support the NPV calculation in two basic ways:
- First, the change in asset value at the end of an analysis period – with discounting applied – can be used to represent the benefits of one investment strategy compared to another.
- Second, the depreciation of an asset each year can be used as a proxy for the benefits consumed by the asset. This can be significant if one has established a non-linear pattern of benefit consumption as described in Chapter 6, or if an asset is fully depreciated in one of the alternatives being evaluated (in which case it yields no benefits compared to an asset with remaining value).
Table 7-4 illustrates the use of asset value in an NPV calculation. The table shows the NPV of an improved asset management strategy, Strategy B, compared to a base case, Strategy A. In Strategy B treatments are performed over the life of an asset, resulting in an increase in cost. With discounting applied, this increased cost total $82 million over 20 years. While Strategy B costs more, it results in greater value at the end of the analysis period: $320 million for Strategy B versus $0 for Strategy A. Applying discounting, the increased value of Strategy B is $146 million. The NPV of Strategy B compared to Strategy A is $64 million, the difference between the increase in value of $146 million and increase in costs of $82 million.
In this example depreciation is assumed to be linear, and thus the same in each alternative. The example excludes consideration of additional factor which may further support an improved asset management approach, such as the increased maintenance cost or potential for asset failure in the case of Strategy A.
Table 7-4. Example NPV Calculation (values in $ millions)
| Year | A: Base Case | B: Improved Asset Management | Discount Factor (4% Annual Discount Rate) | Discounted Change in Costs (B-A) | ||
|---|---|---|---|---|---|---|
| Treatment Cost | Asset Value | Treatment Cost | Asset Value | |||
| 0 | 400 | 400 | 400 | 400 | 1.00 | 0 |
| 7 | 0 | 260 | 20 | 320 | 0.76 | 15 |
| 14 | 0 | 120 | 100 | 380 | 0.58 | 58 |
| 20 | 0 | 0 | 20 | 320 | 0.46 | 9 |
| Discounted Change in Treatment Cost (B-A) | 82 | |||||
| Discounted Change in Asset Value (B-A as of the end of the analyis) | 146 | |||||
| NPV of Improved Asset Management (Increase in Asset Value – Change in Cost) | 64 | |||||
For some applications it can be useful to present a set of multiple measures from the set described above, along with additional context concerning how the measures are defined and should be interpreted. Table 7-5 provides an example set of calculations.
In this example, an asset inventory has an initial value of $120 million. Accumulated depreciation is $30 million, resulting in a current value of $90 (the initial value less depreciation). Based on these figures the ACR is 0.75, or $90 million divided by $120 million.
It is further assumed the $5 million is required annually to maintain value, while $60 million would be required over a 10-year period to achieve the desired state of good repair for the agency. The cost to achieve the desired state of good repair averages $6 million per year. This is higher than the cost to maintain value, which would be expected if current conditions were somewhat less than the desired state of good repair. If projected expenditures are $5 million per year, then the ASR is 1.00 and the AFR is 0.83. ASR is calculated by dividing the annual expenditures by the cost to maintain, while ASR is calculated by dividing 10-year expenditures ($50 million) by the 10-year cost to achieve the desired state of good repair.
Table 7-5. Calculation of Value-Related Measures
| Row | Measure | Value | Notes |
|---|---|---|---|
| 1 | Initial Asset Value ($M) | 120 | |
| 2 | Depreciation ($M) | 30 | |
| 3 | Current Asset Value ($M) | 90 | Row 1 minus Row 2 |
| 4 | Cost to Maintain Value ($M) | 5 | Can be calculated based on annual depreciation or using management systems |
| 5 | Cost to Achieve the Desired State of Good Repair Over 10 Years ($M) | 60 | Should be calculated using the agency’s management systems |
| 6 | Projected Annual Expenditures | 5 | Can be calculated based on annual depreciation or using management systems |
| 7 | Projected Expenditures Over 10 Years ($M) | 50 | Should be based on the agency’s financial plan |
| 8 | Asset Sustainability Ratio (ASR) | 1.00 | Row 6 divided by Row 4 |
| 9 | Asset Consumption Ratio (ACR) | 0.75 | Row 3 divided by Row 1 |
| 10 | Asset Funding Ratio (AFR) | 0.83 | Row 7 divided by Row 5 |
This section provides examples of “emerging,” “strengthening,” and “advanced” practices for the calculation of value and related measures. In the table an emerging practice is one that supports the guidance with minimal complexity, an advanced practice illustrates a “state of the art” example in which an agency has addressed some aspect of the asset value calculation in a comprehensive manner, and a strengthening practice lies between these two levels.
Asset value is calculated for major assets at an aggregate level as required to support financial reporting and TAMP requirements.
Asset value is calculated for major assets. Either the calculations are performed at an asset/component level or supplemental analysis is performed to confirm use of the approach for aggregating asset value calculations.
Asset value is calculated for major assets. Either the calculations are performed at an asset/component level or supplemental analysis is performed to confirm use of the approach for aggregating asset value calculations. Sensitivity analyses are periodically conducted to show the effect of changes in key analysis parameters.
The agency prepares a balance sheet as part of its financial reporting, but does not attempt to reconcile asset value in the financial report with TAM estimates.
Differences in approaches between financial reporting TAM asset valuation are documented as a one-time exercise performed when preparing the TAM asset valuation.
Consistent approaches are used where possible to prepare the balance sheet in the agency’s financial report and value assets for TAM. Differences in approaches are resolved where possible, and regularly reviewed and documented in financial and TAM reports where they remain.
Cost to maintain current value, ASR and asset ACR are or can be calculated using annual depreciation and expenditures.
Cost to maintain current value, ASR and asset ACR are or can be calculated using annual depreciation and expenditures. In addition, supplemental analysis is performed using the agency’s management systems to establish the cost to maintain current value.
Cost to maintain current value, ASR, ACR and AFR are calculated and used to support investment decisions. Supplemental analysis is performed using the agency’s management systems to establish the cost to maintain current value and the cost to achieve the desired state of good repair.
This section summarizes the potential applications of asset value to support TAM. Section 8.1.1 organizes these applications into a set of key questions. Section 8.1.2 details which of the measures presented previously support answering the different questions.
As discussed in Section 2.1, asset value and measures related to asset value can be used to support a variety of TAM-related decisions. This section expands the discussion of potential applications of asset value in Section 2.1 through defining a set of six key questions that an asset owner may wish to use asset value to help address. These are as follows:
- What is the overall value of the asset inventory? This is the most fundamental question one might ask about asset value. That is, given an inventory of assets, what exactly is their value? Typically, one seeks to answer this question at a high level, such as for all pavements on the NHS, rather than for specific assets. However, even at a high level it helps put all of an agency’s TAM decisions into perspective, establishing the importance of focusing on inventory maintenance. Further, answering this question supports compliance with Federal regulations requiring State DOT TAMPs to detail the value of NHS pavement and bridges. While the Federal requirement is to calculate current value, one may seek to calculate further historic value and/or predicted future value given a set of assumptions about asset funding, use, deterioration and other parameters to provide further context for TAM decisions.
- What is the cost to maintain current asset value? Establishing overall asset value for each asset classification is a prelude to this follow up question. Here, one seeks to determine how much value is lost each year as assets age, and what investments are needed to offset depreciation and optimize the assets’ lifespans. Value is preserved or restored as a function of the treatments performed on existing assets, or as new assets are constructed. As in the case of the first question, asking and answering this question helps put TAM decisions into context. It helps justify whether a given set of TAM investments are defensible. Information on the cost to maintain asset value can guide an agency to establish the necessary level of investment for preserving its existing assets. Also, answering this question supports compliance with the Federal TAMP regulation, which requires that State DOT NHS TAMPs document the cost needed on an annual basis to maintain value of NHS pavements and bridges. One can compare this cost to an agency’s planned expenditures to establish whether asset value, and by extension asset condition, is expected to increase, decline or remain the same.
- How much should we spend on our existing assets? This question is closely related to the second question, but the two questions may have different answers. If the measure of value is meaningful, then an agency should ideally spend enough money to maintain or increase asset value over time. However, it is inevitable that the value of a given asset will decline following construction or renewal of the asset: it is simply not realistic to expect assets to remain in a “like new” condition indefinitely. On the other hand, if the value of the asset inventory has declined to the point that is demonstrably suboptimal (e.g., a case in which assets are in such poor condition that users experience increased costs from delay and the agency incurs increased costs from emergency maintenance) then merely maintaining such a suboptimal condition is undesirable. Thus, answering this question requires additional analysis to determine the asset value associated with achieving an agency’s “desired state of good repair,” and the cost to achieve this value. Once obtained, the answer supports decisions about how much to invest in the asset inventory.
- How should funds be allocated between different assets or networks? To the extent that funds are insufficient for addressing all of an agency’s investment needs, it may be necessary to prioritize between different asset classes or networks (e.g., the Interstate System, Non-Interstate NHS, and Non-NHS). Information on asset value helps communicate the size of the inventory expressed in a single unit of measure – dollars. It also illustrates the impacts of different budget allocations. If the measure of value is constructed such that it is proportional to the economic value of the asset inventory, then one can demonstrate that an investment approach which maximizes value across asset classes and networks also maximizes societal benefits.
- What’s the best life cycle strategy for our assets? Information on asset value, together with supporting management systems, can be used to test different asset lifecycle strategies and illustrate the effectiveness of different strategies for maximizing value. Doing this requires predicting asset value assuming different strategies and comparing their results. For instance, one can compare a proactive strategy, in which interventions are performed over time to achieve or extend the expected asset life, to a more reactive strategy, in which few or any interventions are performed, shortening asset life. To perform such an analysis, one must adjust asset life assumptions for each scenario and/or base depreciation on changes in condition rather than asset age. Note that while asset value can help support decisions about asset life cycle strategies, a management system is needed to develop potential lifecycle strategies and determine what specific interventions are needed for a given asset.
- What is the value generated by the asset? Much of the discussion thus far has revolved around the value of the asset, as it relates to construction and maintenance costs. However, two assets of the same type, length, and roadway characteristics, may generate strikingly different value for the communities that use them. Variations in the volume of traffic, the availability of alternative routes, and the accessibility offered by these roads are only some of the factors affecting how road users perceive their value. For example, a road user whose next best alternative adds an additional hour to their commute will value the presence (and maintenance) of that road much more highly than the user with several equidistant alternative routes. When considering investment decisions, it is important to account for the road user’s perspective. The ISO asset management standard (1) includes further discussion of this topic.
The different measures presented in Chapter 7 may be applied to answer the key questions posed above. Table 8-1 is a matrix showing which measures can help answer each of the six questions listed above. With the exception of the first question, all others require one or more supporting measures that are derived from asset value.
Table 8-1. Asset Value-Related Measures and Mapping to Key Questions
| Key Questions | Asset Value | Cost to Maintain Current Value | Asset Sustainability Ratio (ASR) | Asset Consumption Ratio (ACR) | Asset Funding Ratio (AFR) | Net Present Value (NPV) |
|---|---|---|---|---|---|---|
| Q1: Overall Inventory Value | X | X | ||||
| Q2: Cost to Maintain | X | X | X | |||
| Q3: Needed Spending | X | X | ||||
| Q4: Allocating Funds | X | X | X | X | X | |
| Q5: Life Cycle Strategy | X | |||||
| Q6: Value Generated | X |
This section provides guidance for using asset value to support the applications summarized in Section 8.1. For each application it discusses pertinent considerations in the asset value calculation, notes relevant issues in interpreting the results, and provides one or more examples of agency practices.
The fundamental use of asset value is to communicate what assets an agency owns using currency as the common units across asset classes and components. All of the approaches for calculating value support this application.
Two examples of agency practice for communicating value in a TAMP are provided in Chapter 2: the City of Melbourne’s approach integrating asset value with other measures in a graphical view (7), and the approach used by Carver County, Minnesota to summarize asset replacement cost and current value in a table listing the different asset classes addressed in the TAMP (8).
Considerations for using asset value to summarize an agency’s inventory and current condition are as follows:
- Given there are different approaches for calculating value, it is important to summarize the basis for the value calculation – e.g., based on current replacement cost or historic costs.
- While all of the value approaches can be used for this application, as a practical matter, approaches based on the cost or market perspectives are preferred given they are easiest to calculate, communicate and explain. Regarding the cost perspective, current replacement cost is preferred over historic costs as the use of historic costs unadjusted for inflation may understate value from the perspective of an asset manager.
- The calculation of overall asset value lends itself to parsimonious approaches, such as performing the value calculation at a network level and avoiding calculations for any asset classes or components that would ultimately be aggregated when presenting the results. More granular details in the calculations should be introduced only if they are necessary to obtain an accurate overall value, or if they will help support other asset value applications.
- Where feasible, both the initial or “like new” value and current asset value should be communicated to distinguish between the potential value of the agency’s assets and the value given their remaining life. Any of the approaches discussed in Chapter 6 can be used to calculate depreciation in this case if a calculation is needed.
- When summarizing value across multiple asset classes, care should be taken to avoid double-counting asset value. Often the calculation of value for a complex asset includes multiple classes of assets. For instance, the value calculation for pavement may include costs for traffic and safety features such as signs, traffic signals and guardrails, and land. The calculation for track may include signals, electrification, small structures, and land. Before adding another asset class to the calculation, it is important to verify that its value has not already been included as part of another class.
The cost to maintain current asset value can be calculated using any of the asset valuation approaches. However, this measure is best supported when the initial asset value is calculated using current replacement cost or market value, and when depreciation is calculated using a condition-based approach. Also, to support an accurate calculation, assets should be represented at a sufficient level of detail for quantifying the costs and effects of major capital expenditures. In many cases this may suggest a need for defining asset components for bridges, facilities and/or other complex assets where a capital investment may focus on one portion of an asset.
As discussed in Chapter 7, the preferred approach for calculating the cost to maintain asset value uses an agency’s asset management systems to define a funding scenario in which conditions are maintained, and then use this scenario as the basis for stating the cost to maintain value. However, where this approach is impractical, the alternative is to calculate annual depreciation, and use this as an estimate of the cost to maintain.
If the asset valuation approach is overly simplified, then annual depreciation may prove to be a particularly poor proxy for the cost to maintain. For instance, if asset value is measured strictly based on historic costs and asset life is assumed to have a constant rate of decrease without regard to level of maintenance, then this limited approach would lead to a cost for maintaining value that is simply an equal amount each year, adjusted for annual inflation. Finding the appropriate level of detail in the valuation process has a great impact on how the valuation may be used.
Regardless of the specific approach for obtaining the cost to maintain, it is recommended that this measure be accompanied by ASR, defined here as planned expenditures divided by the cost to maintain current value. ASR is not a cost at all, but a ratio. Nonetheless, it is a useful measure for evaluating whether or not an asset owner is investing the necessary amount to maintain value, regardless of what that cost actually is.
Chapter 2 includes a description of the approach for reporting pavement ASR used by Washington State DOT (WSDOT) (10). This agency uses an approach described by FHWA (43) to estimate the additional life added to the system through pavement treatments and divides this by the life through deterioration to calculate ASR. This approach to calculating ASR does not involve an explicit calculation of ASR, but is consistent with the definition of the measure presented in Chapter 7.
Issues to consider when reporting the cost to maintain current asset value include:
- The approach used to calculate the measure should be noted because it impacts the potential applications of the cost and/or ASR.
It is important to clearly communicate what types of costs are included in the cost to maintain current value, and what types are excluded. For instance, it is common to exclude preventive maintenance costs from management system models and depreciation calculations, while assuming these activities will nonetheless continue to be performed. If annual depreciation is used, then the costs that are included will depend upon the specific set of treatments one has defined, as described in Chapter 5.
- If an agency has determined that following its life cycle strategies and achieving its desired state of good repair requires maintaining current conditions, then the cost to maintain current value may be the same as the amount of spending needed. Otherwise, the two may be different, such as when greater levels of spending are needed to maintain current value or when additional investment is needed to increase asset value. However even when the values are different it can be instructive to show both the cost to maintain and total need.
Determining the amount of money an agency needs to spend on its assets is inherently subjective. The calculation depends on the answer to the question “what constitutes a need?” and this question has many potential answers.
The Federal definition of asset management provides an approach for addressing what asset investments are defined as needs. The TAMP regulation (23 CFR 515.5) defines asset management as a process for identifying “…a structured sequence of maintenance, preservation, repair, rehabilitation, and replacement actions that will achieve and sustain a desired state of good repair over the life cycle of the assets at minimum practicable cost.” The regulations further require that agencies define a set of asset management objectives aligned with this definition, and perform a gap assessment relating actual conditions to agency two and four-year performance targets and the desired state of good repair. Once this desired state of good repair is established, the asset owner must establish which treatments are required to achieve and maintain the desired state at minimum cost.
The GASB 34 modified approach (1) provides similar flexibility. Agencies using the modified approach do not calculate depreciation for their infrastructure assets. Instead, they define a target level of service, and determine the cost to maintaining the target level. Provided the agency continues to maintain their assets at the target level of service, they can state the cost of maintaining the target level of service as an operating cost in their financial reports in lieu of depreciation.
The approach recommended here for establishing the level of investment needed for a set of assets is meant to be consistent with U.S. Federal TAMP regulations and the GASB 34 modified approach. That is, the asset owner should clearly define their desired state of good repair, and then base their calculation of needed funding on the funding required to achieve and maintain this state. This information can then be used to calculate and report AFR, planned funding divided by needed funding over a 10-year period.
However, how does required spending relate to asset value? In many cases, the needed level of spending will be similar to, if not the same as, the cost to maintain asset value. As discussed above, the two measures are not the same, but for a mature asset inventory that has reached a steady state and is being maintained in its desired state of good repair, the two may be very similar. Annual depreciation provides a rough approximation of the cost to maintain value, and thus may provide an approximation (albeit an even rougher one) of needed spending. Even when needed spending, the cost to maintain, and annual depreciation are all different, it can be helpful to communicate the three values and the differences between them to make the case for any necessary investments.
In the case where economic perspective is used as the basis for calculating asset value, an alternative approach may be appropriate for defining an assets’ needs and the cost to meet them. Any asset investment with a positive NPV provides a benefit to users and therefore may be considered needed by the agency. The cost of meeting needs is then the cost of performing all investments with a positive NPV over a defined period. This requires that the NPV calculations include other treatments for complex assets, such as rehabilitation of pavement, bridges and facilities.
The example below shows how one agency has addressed the challenge of defining asset need. The Vermont Agency of Transportation (VTrans) summarizes needed funding in its TAMP using ASI (similar to AFR) and ACR (44). In its TAMP, VTrans uses the results for these measures to illustrate the impact of planned funding levels and show that available funding is less than what is needed to meet the agency’s needs.
VTrans defines asset sustainability index (ASI) as “the ratio of anticipated needs to anticipated revenues”. ASI demonstrates the percent of maintenance needs met by projected funds. ACR is used to weigh the impact of investment decisions on overall asset value.
VTrans develops graphs and tables to illustrate the transformation of the ASI under different scenarios. In the graph below, the blue bars reflect a 0% revenue growth scenario, the yellow bars indicate a 2% growth scenario, and the green bars represent a 4.5% growth scenario. The ASI clearly demonstrates how the agency will face growing funding deficits unless the budget is increased.
The VTrans TAMP includes tables displaying the ACR for bridge and pavement assets, see the 6th column in the table. By comparing the size of the investment with the resulting change in ACR, VTrans contextualizes the impact of each investment. The ACR is also used to identify which assets are in need of future investment. When a small percent of the asset’s life remains, more funds should be committed to renewing the asset or asset class.
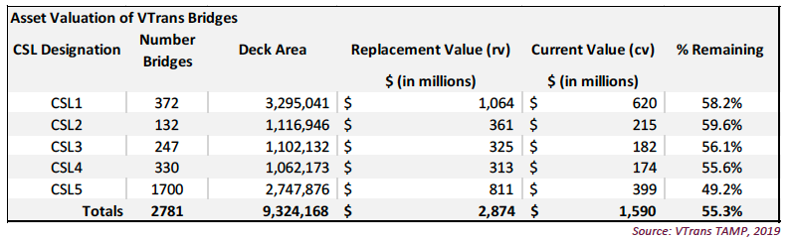
Source: Vermont Agency of Transportation (44)
Issues to consider when determining needed funding include those identified previously for calculating the cost to maintain asset value. An additional consideration is the timeframe of the projection. An analysis period of 10 years or more is recommended when determining needed spending and AFR given there may be large variations in year-to-year spending which can obscure trends.
Information on asset value does not provide a direct indication of how an agency should invest in its assets. Ideally, an agency should use its management systems to define and select scenarios reflecting their preferred allocation of funding. However, asset value and related measures can clarify conditions and trends between different asset classes and groups of assets to support resource allocation decisions. For instance, an agency might show that increased investment is needed for a given asset class or system based on the asset’s overall value, the gap between current spending and spending needed to maintain asset value, a(nd/or other value-related measures.
All of the different approaches for calculating asset value can support decisions about how to allocate funding. However, asset value is most likely to relate to asset funding and conditions when:
- Complex assets are valued at a component level;
- Initial asset value is based on current replacement cost or market value;
- Effects of major treatments that improve asset condition are included in the calculation; and
- Depreciation is condition-based and condition data are collected and used for supporting allocation decisions.
The callout box shows an example of how asset value can support resource allocation tools. It describes the Structures Asset Valuation and Investment (SAVI) Tool developed by the UK Department for Transport (45). The SAVI Tool is a spreadsheet tool that stores data on an inventory of bridges at the component level, calculates asset value using depreciated replacement cost, helps define a lifecycle strategy for bridges, and predicts future costs and conditions based on the selected lifecycle strategy. The tool includes a summary of asset value for different groups of bridges to support financial reporting and provide insights into recommended funding.
The SAVI tool is used by transportation practitioners in the UK to complete structural valuations, calculating replacement cost, depreciated replacement cost, accumulated depreciation, and annual depreciation values. The tool provides a consistent, national approach to managing and valuing asset structures based on the condition of the structures’ component elements. The tool’s beta testing finished in October 2019, and it was formally released at the Bridges 2020 conference in Coventry.
The SAVI tool uses the methods of valuation defined in Chartered Institute of Public Finance and Accountancy (CIPFA) guidance. Replacement cost is calculated using a unit cost per square meter, and depreciation is dictated by deterioration curves which provide an effective element age. Using these valuations, SAVI can develop long-term asset management plans (AMPs) up to 120 years, short-term plans up to five years, and intervention strategies. It can also model different budget scenarios.
The tool was designed in response to local agencies recognizing their need for a database to manage their asset inventory data which can return useful outputs and analysis. The SAVI tool supports several types of structures including bridges, culverts, tunnels, underpasses, lighting, retaining walls, road signs, signals, and reinforced earthworks. For each of these asset types, it requires detailed inventory and condition data as well as anticipated expenditures on routine and special maintenance. The tool can analyze up to 5,000 structures at once.
Three dashboards one for the valuation, one for the short-term AMP, and one for the long-term AMP supply summaries of the asset analysis and document the projected condition-based maintenance expenditures. A sample graph from the LAMP dashboard is included below. Additionally, a fourth page reports the element condition score for every element in the model for each year of analysis; it highlights when assets fall into disrepair and which assets are maintained in good condition.
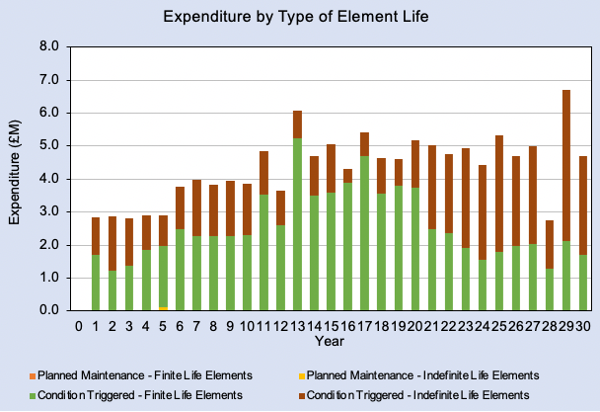
Source: UK Road Liaison Group (45)
Asset value can provide useful supporting information when developing the strategy for maintaining an asset over its life cycle, as illustrated in the case of the SAVI Tool described here. Further, asset value can be used explicitly to compare life cycle strategies in two ways:
First, if an economic perspective is used as the basis for value, then calculations of asset value yield the NPV of an asset over its life cycle. NPV provides a quantitative measure that can be used to compare different scenarios to establish the preferred life cycle strategy for an asset. To compare different life cycle strategies, the asset valuation must meet the additional requirement of distinguishing between the different treatments being considered, such as rehabilitation treatments for pavements, bridges, facilities and other complex assets.
Alternatively, if a cost or market perspective is used as the basis for value, asset value can be used as the residual value of an asset for calculations of asset life cycle cost, as illustrated in the example in Chapter 2. This provides an approach for quantifying the differences between two strategies where one strategy results in a different remaining life or condition at the end of the analysis period.
The Transit Asset Prioritization Tool (TAPT) included with TCRP Report 172 (46) illustrates use of asset value – or more specifically, the NPV of an asset – to establish a life cycle strategy. The tool is described in the callout box. The tool recommends a simplified life cycle strategy for each asset class (that is, when to replace the asset) based on the NPV of the asset. The strategy with the lowest NPV is selected for each asset class. In addition, the tool reports total NPV for all assets when generating scenarios of future asset conditions.
The Transit Asset Prioritization Tool (TAPT) is an analytical tool for analyzing and prioritizing investment needs for maintaining transit assets in a state of good repair. The tool includes three types of asset models: a mileage-based model intended for use with revenue vehicles; a condition-based model for use where an asset’s remaining life can be approximated based on condition; and an age-based based model for other asset classes. The tool user creates a set of asset class models using the three model types.
Each asset model predicts the agency and user costs associated with an asset over its life cycle. Also, the models predict when to replace an asset. The benefit of replacement is calculated as the increase in NPV that results from from replacing the asset at a given age relative to deferring replacement for one year. TAPT uses the asset class models to predict asset investment needs, and simulate conditions over time given a specified budget. One of the measures predicted for an analysis is the NPV of asset investments simulated as occurring in each period of the analysis.
Source: TCRP Report 172 (46).
The final application of asset value for supporting TAM is the calculation of the value derived from an asset. Often times an asset manager is not specifically concerned with this question, because in many instances it may be taken as a given that the assets one manages are, indeed, necessary and important, and the asset manager cares primarily about how best to manage a set of assets given this assumption. However, in some cases the asset manager may be specifically interested in the value derived from one asset versus another and/or whether a given asset merits further investment. For example, when considering how to prioritize assets for resilience investments, one may wish to consider the degree to which different potential assets will reduce the likelihood of risk and the consequences of a possible asset failure, with consequences quantified based on the value of the asset to society.
The callout box provides an example of how the value from a set of assets can support TAM. The Return on Investment (ROI) Calculator described in TCRP Report 206 (47) calculates the overall ROI of planned investments to achieve a state of good repair for transit assets. The tool allows one to compare different investment scenarios, producing measures of investment including NPV, Benefit Cost Ratio (BCR), and Internal Rate of Return (IRR).
Determining the “value from” is the central issue that the economic perspective of asset value is intended to address. Thus, for further discussion of this application the reader should refer to the discussion in Chapter 4 and the supporting appendices.
TCRP Report 206 presents a framework and approach for calculating the return on investment (ROI) of investments in transit assets to achieve and maintain a state of good repair. The report describes how to calculate the value of transit asset investments to a transit agency, transit system users, and society. It includes an ROI calculation tool one can use to calculate and compare different investment scenarios, such as to compare a scenario in which assets are maintained in good repair to one in which asset investments are deferred. Measures calculated using the tool include NPV, Benefit/Cost Ratio, Internal Rate of Return and Payback Period.
Source: TCRP Report 206 (47)
This section provides examples of “emerging,” “strengthening,” and “advanced” practices for using asset value and measures related to asset value to help support TAM. In the table, an emerging practice is one that supports the guidance with minimal complexity, an advanced practice illustrates a “state of the art” example in which an agency has addressed some aspect of the asset value calculation in a comprehensive manner, and a strengthening practice lies between these two levels.
Asset value is reported in agency documents, including financial reports and the agency’s TAMP, but approaches used in different documents may be inconsistent.
Asset value is reported in agency documents, including financial reports and the agency’s TAMP. Discrepancies between different estimates are documented.
Asset value is reported in a consistent manner in different agency documents, including financial reports and the agency’s TAMP. Multiple approaches for reporting value are used as needed to maintain consistency between documents while satisfying reporting requirements.
The cost to maintain current asset value is calculated using annual depreciation and reported in the agency’s TAMP.
The cost to maintain current asset value is calculated using the agency’s management systems. The cost to maintain and ASR are reported in the agency’s TAMP.
The cost to maintain current asset value is calculated using the agency’s management systems. The cost to maintain and ASR are reported in the agency’s TAMP. The cost to maintain and ASR are reviewed when establishing asset investment levels.
Needed funding is reported in the agency’s TAMP. Needed funding is assumed to be equal to the cost to maintain current value.
A separate analysis is performed using the agency’s management systems to support the calculation of the funding needed to achieve and maintain the agency’s desired state of good repair.
A separate analysis is performed using the agency’s management systems to support the calculation of the funding needed to achieve and maintain the agency’s desired state of good repair. Needed funding is considered in establishing asset investment levels.
Asset value is reported by asset class and system in the agency’s TAMP or supporting documents.
Asset value and supporting measures such as the cost to maintain current condition, ASR, AFR and ACR are reported by asset class and system in the agency’s TAMP or supporting documents.
Asset value and supporting measures such as the cost to maintain current condition, ASR, AFR and ACR are reported by asset class and system in the agency’s TAMP or supporting documents. Information on asset value and related measures is used to support decisions concerning the allocation of funding between asset class and system.
The NPV of different potential life cycle strategies is explicitly calculated when selecting asset life cycle strategies.
The NPV of different potential life cycle strategies is explicitly calculated when selecting asset life cycle strategies. Asset value is used as a component of life cycle cost, such as for quantifying the residual value at the end of the analysis period.
The NPV of different potential asset life cycle strategies is explicitly calculated when selecting strategies. The calculation includes relative impacts to travelers and society for different life cycle strategies, such as changes in travel time or operating costs.
The overall value from an agency’s assets is calculated to help establish the overall value of the assets to travelers and society.
The overall value from an agency’s assets is calculated. The calculation considers changes value related to asset age or condition.
The overall value from an agency’s assets is calculated. The calculation considers changes value related to asset age or condition. Further, the calculation is used to support decisions about agency investments in relevant applications such as selecting resilience investments.
This section details a set of worked examples illustrating application of the asset valuation guidance presented in Chapters 3 to 8. The examples include calculation of asset value for: 1.) a highway agency based on cost and market perspectives; 2.) a transit agency based on a cost perspective; and 3.) a highway agency based on an economic perspective. The examples are drawn from a set of four validation tests performed using a draft version of the guidance. Together, the examples illustrate the application of many of the different concepts and options described in the previous chapters, including different perspectives on what value represents, different approaches for calculating initial value, and different approaches for calculating depreciation.
Note that the data from the agencies participating in the testing has been adapted for the purpose of providing examples. In some instances, data from different validation tests have been combined or simplified to best illustrate the asset value calculation process.
In this example, a highway agency in the Northern U.S., labeled “The Northern Agency,” is interested in calculating asset value and related measures to report for highway-related assets in its TAMP. Note, this example is adapted from tests with two different agencies, and is not intended to be representative of any actual agency.
Following the process outlined in Section 2, the agency first establishes that its goal is to establish overall value and related measures for three asset classes: pavement; structures (including bridges and bridge-length culverts); and buildings. The agency has data at the asset-level for each asset class. For pavement and structures, the agency has detailed condition data. For buildings, the agency has only summary inventory data, but its facility division has separately established insurance values representing the amount each building is insured for in the event of a catastrophic event, independent of the value of land or the equipment in each building.
For their structures, the agency decides that asset value should be computed at a component level, given that different structure components have different useful lives and condition data are available to support the calculation. Bridges are represented using three components: the bridge deck, superstructure and substructure. Bridge-length culverts are represented as a single component.

The following subsections describe the approach used for Steps 2 to 4 of the asset value calculation by asset class, followed by a summary of the results.
Pavement
Using the flow chart in Chapter 4 the agency decides that initial value for pavement should be based on replacement cost, given there is no need to maintain consistency with the approach used for financial reporting (based on historic costs), no specific need to calculate value of the asset class to society (which would suggest a need for calculating economic value), nor is there a market value that may be readily determined as an alternative.
Next, the agency reviews its treatment strategy for pavements. Initial construction of pavement is estimated to cost $1.4 million per lane mile. When a pavement section reaches the end of its useful life it is reconstructed at a cost of approximately $1 million per lane mile, restoring it to “like new” condition. Various treatments are performed over a pavement’s life, and their effects are reflected in the Pavement Condition Index (PCI) at any given time. PCI is an agency-specific measure of pavement condition. It combines different pavement distresses into a scale from 0% (worst condition) to 100% (best condition).
Given their use of the replacement cost approach to calculate initial value and PCI to capture condition, the agency determines it is not necessary to incorporate other treatments in the calculation of asset value besides pavement construction and reconstruction. Based on the agency’s life cycle strategy, the pavement is deemed to reach the end of its useful life when its PCI is reaches a value of 25%, which typically occurs at an age of approximately 25 years, as depicted in the deterioration curve shown in Figure 9-2. The pavement assets’ residual value is estimated to be $0.4 million per lane mile, equal to the difference in cost between initial construction and reconstruction.
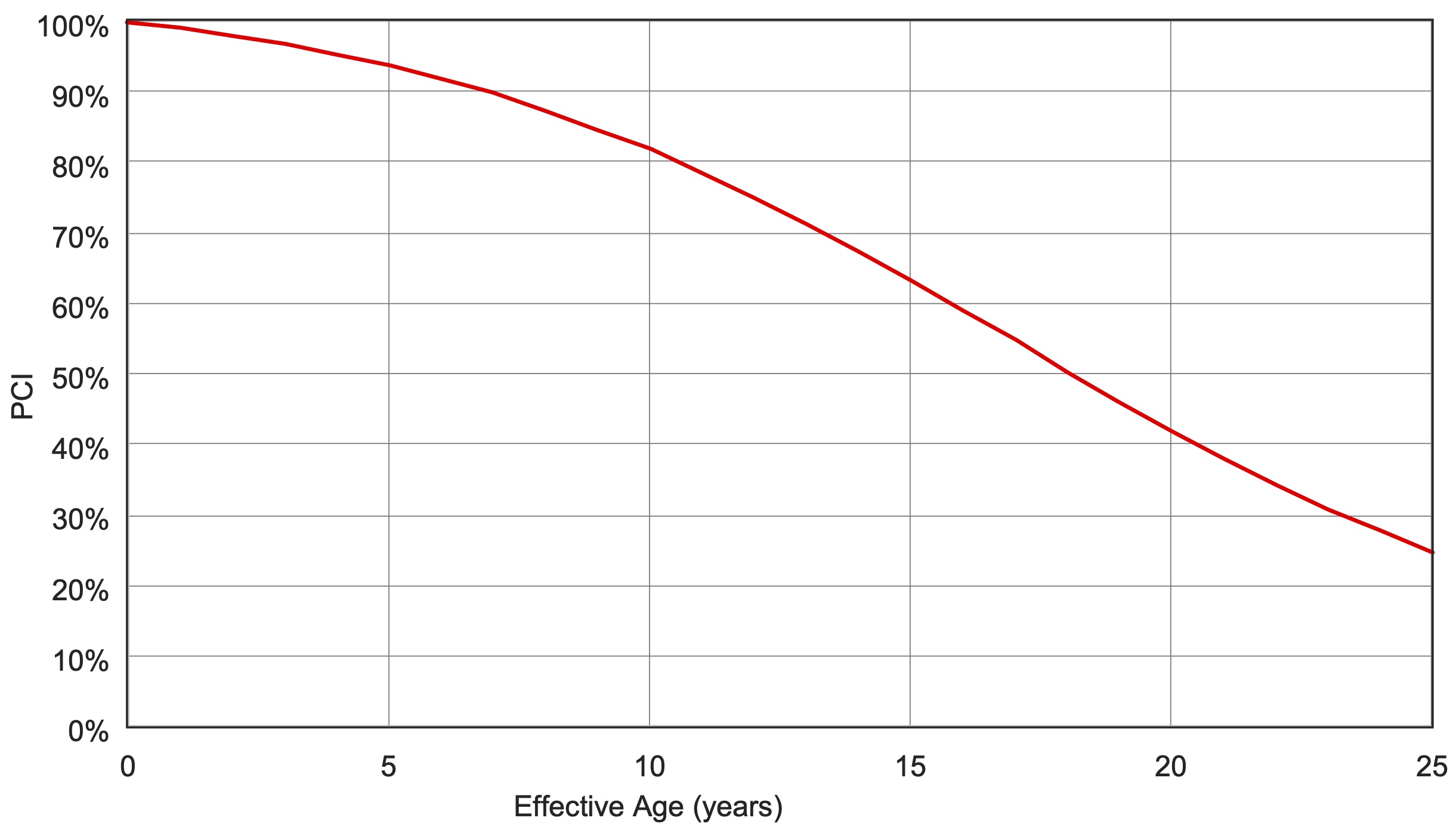
Then, the agency considers how to calculate depreciation. Reviewing the flow chart in Chapter 6, the agency decides to use a condition-based approach for calculating depreciation. The PCI of a pavement section estimates the effective life remaining where condition data are available. Where data are unavailable, the asset’s actual age is used. Figure 9-3 summarizes the distribution of pavement condition, depicting the percentage of pavement lane miles for each effective age from zero to over 24. Most of the assets have an effective age of under five years.
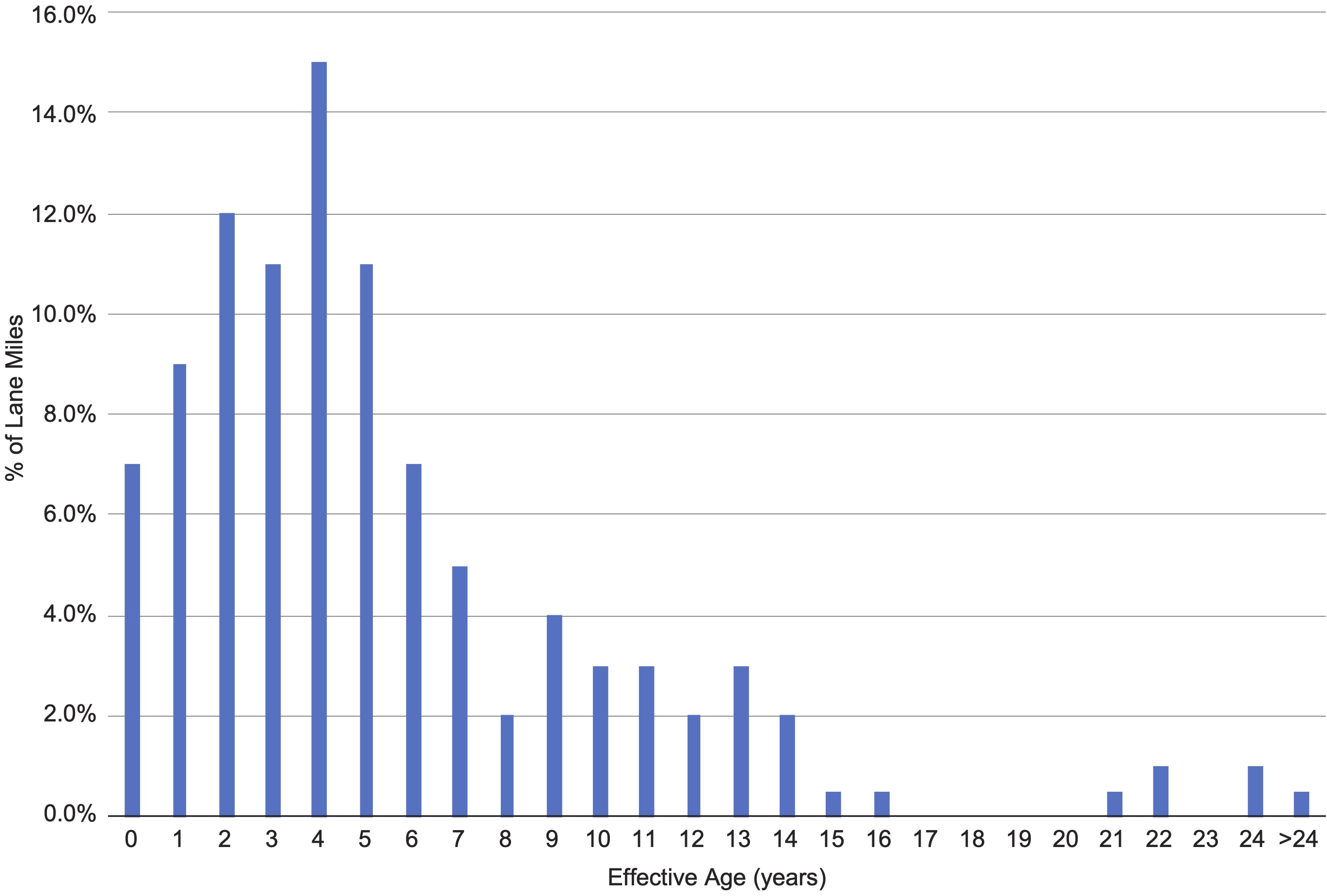
The agency uses the above information to calculate the value of its pavement. Initial value is approximately $30.8 billion (22,000 lane miles x $1.4 million per lane mile). For each section, depreciation is calculated based on the effective age using the depreciation formula for the condition-based approach, provided in Chapter 6. The result is that current pavement value is calculated as $26.0 billion with annual depreciation equal to $876 million. Annual depreciation is calculated by aging each pavement section by an additional year and noting the resulting change in value.
Structures
After completing the pavement valuation, the agency walks through the same process outlined above for structures, considering each of the bridge components defined. As in the case of pavement, the agency decides that initial value should be based on replacement cost.
The agency next reviews its treatment strategy for bridges and bridge length culverts. The construction of a bridge or culvert costs approximately $280 per square foot of deck area. Replacing a structure has a similar cost. The approximate costs for replacing bridge decks, superstructures and substructures are established based on a pro-rated share of the total bridge replacement cost, considering the relative costs of replacing the component parts. Based on these historic costs, the bridge deck replacement is estimated to be 25% of the value of the bridge, the superstructure is estimated to be 40% of the value, and the substructure is estimated to be 35% of the value. Various treatments are performed over the life of a component, and their effects are reflected in the component conditions ratings. These are measured on the 0 to 9 scale defined for the NBI. When a component has reached the end of its useful life either the component is replaced or the entire structure may be replaced.
Given the incorporation of the component condition ratings into the NBI, the agency determines it is not necessary to include any treatments in the calculation of asset value besides initial construction and component or bridge replacement. Based on the agency’s life cycle strategy, a bridge deck is deemed to be at the end of its useful life when it has a rating of 4 or less on the NBI scale. For the superstructure, substructure and culverts, the component is deemed to be at the end of its useful life when it has a rating of 3 or less. Figure 9-4 illustrates the agency’s deterioration curves depicting the effective age of a component as a function of its condition rating. The agency developed these curves for use in their management systems based on an analysis of historic bridge inspection data. Three curves are shown in the figure: one for decks; a second used for both superstructure and substructure; and a third curve for culverts.
The agency further establishes that a portion of its bridges are built to outdated functional standards for load capacity and clearances. These bridges are deemed to be at the end of their useful life regardless of their physical condition. Thus, these bridges are treated as fully depreciated when calculating their asset value.
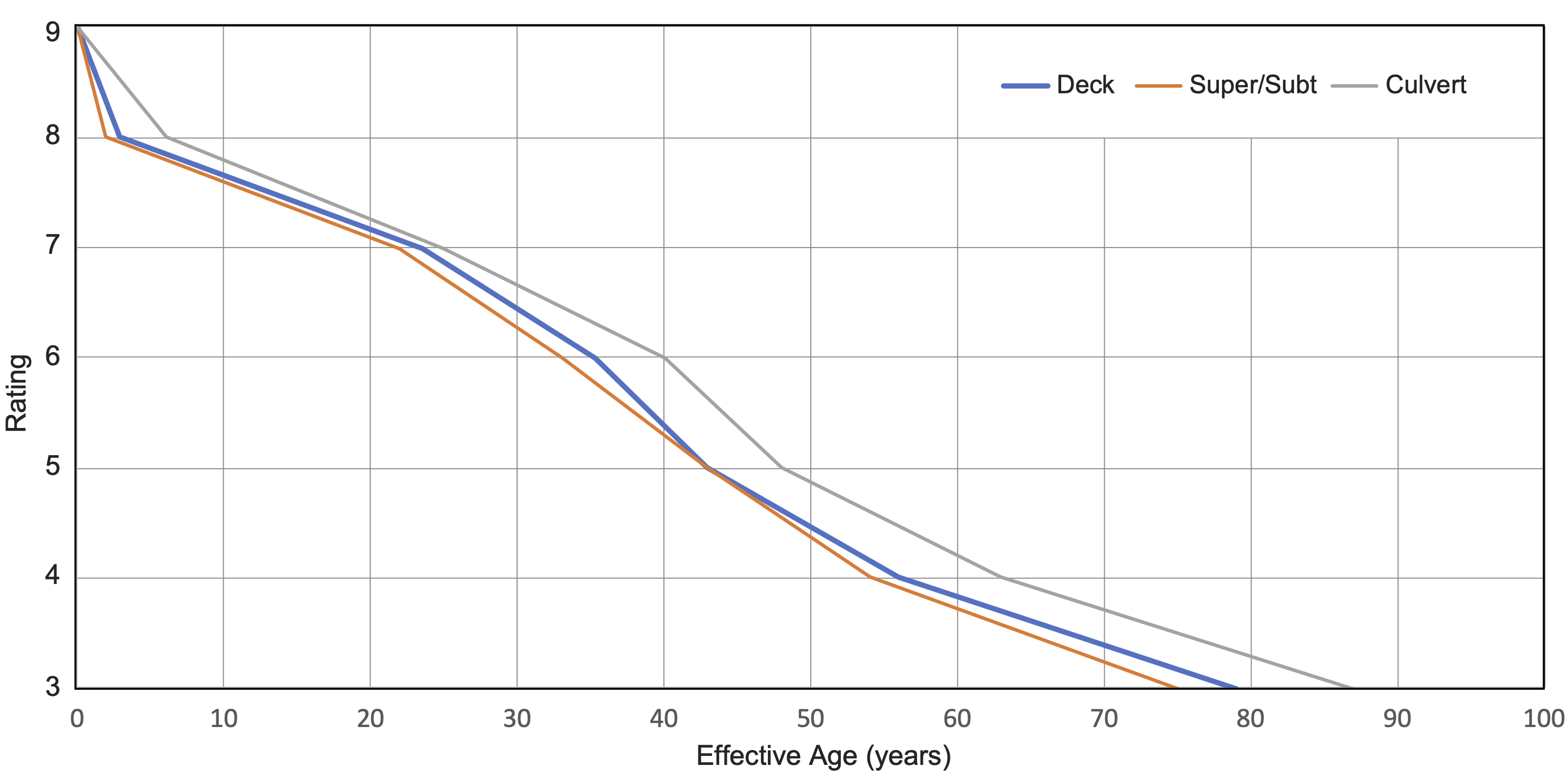
The agency then considers how to calculate depreciation. As in the case of pavement assets, the agency decides to use a condition-based approach. The NBI component rating is used to establish effective age. Figure 9-5 summarizes the distribution of conditions, depicting the percentage of each component in each condition rating (exempting functionally obsolete structures).
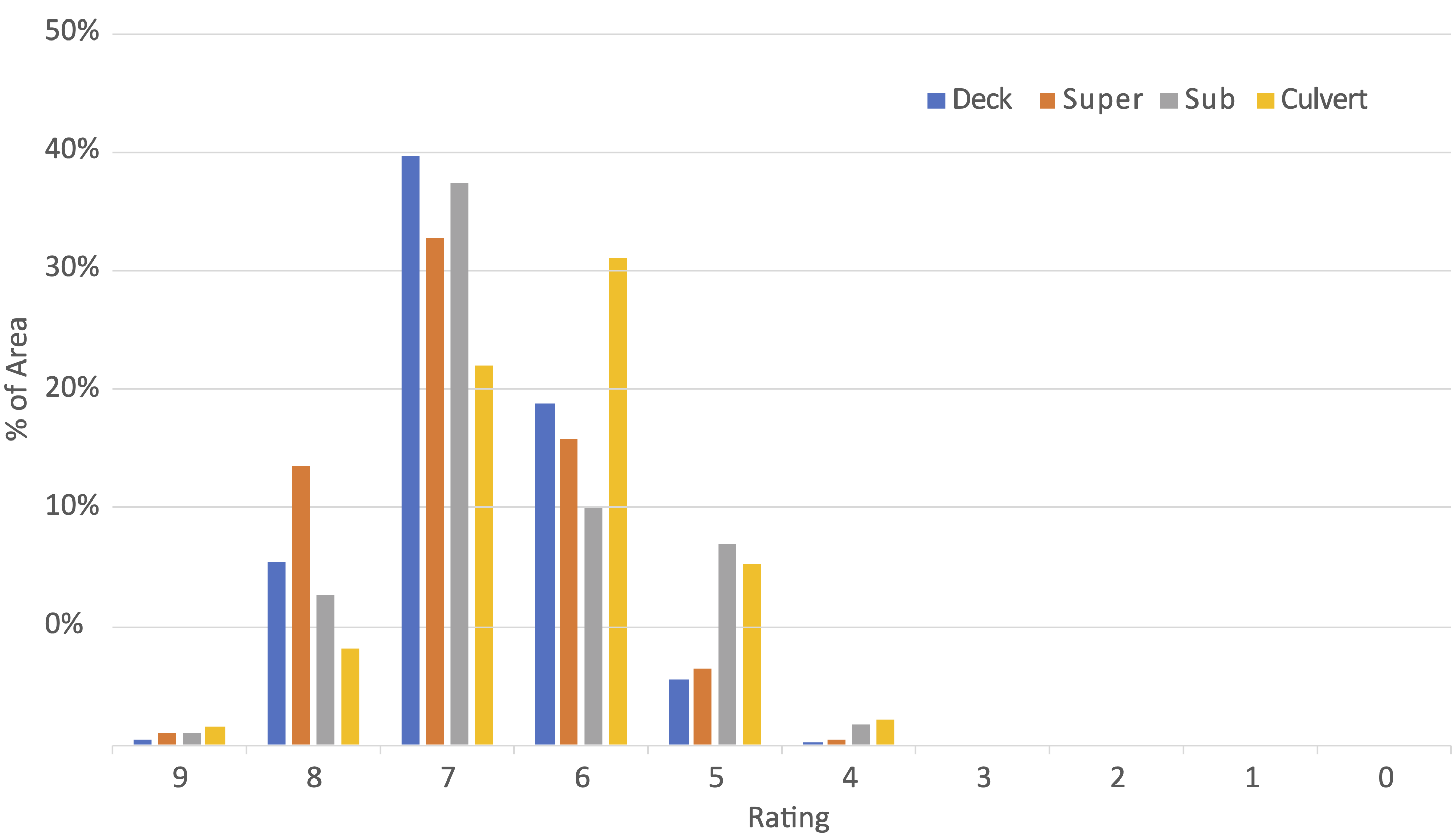
Lastly, the agency uses the approach described above to calculate value. Initial value is approximately $14.0 billion (50 million square feet x $280 per square foot). The calculations of current value are made by component, grouping all of the components of a given rating together (and exempting the obsolete bridges). For each rating group, effective age is estimated using the agency’s deterioration curves, and then depreciation is calculated based using the depreciation formula provided for the condition-based approach in Chapter 6. The result is a current structure value of $8.8 billion. With annual depreciation equal to $193 million; this can be calculated by aging each group by an additional year and noting the resulting change in value.
Buildings
For its buildings, the agency has more limited condition data than it has for pavement and structures. However, as noted above, in addition to its data on the building inventory, the agency has data on the insured value of each of its buildings. The agency decides to use this insured value as a proxy for market value. The agency thereby establishes that the insured values of its buildings totals $0.9 billion.
The agency establishes the cost to replace all of its buildings would be approximately $1.2 billion, and that buildings are estimated to have a useful life of 60 years. The agency determines that an age-based approach should be used for depreciation if it is necessary to further depreciate the market value. Annual depreciation is estimated at approximately $20 million (equal to the replacement cost of $1.2 billion divided by the useful life of 60 years).
Results Summary
Table 9-1 summarizes the results of the asset value calculation. For each asset class, it shows the replacement cost, current value, ACR, and annual depreciation. The total replacement cost for all of the Northern Agency’s highway assets totals $46 billion. Considering the effects of depreciation, the current value of the inventory is $35.7 billion, resulting in an ACR of 0.78. Note there is no specific target value for ACR, but ideally this measure is maintained or increased over time. Absent investment to increase asset value, the inventory is expected to depreciate approximately $1.1 billion per year. This estimate of annual depreciation can be used as an estimate of the Cost to Maintain Value, though as described in Chapter 7 this cost should ideally be calculated using an agency’s asset management systems.
Table 9-1. Summary Results for the Northern Agency
| Asset Class | Subclass | Replacement Cost ($ billion) | Current Value ($ billion) | Asset Consumption Ratio (ACR) | Annual Depreciation |
|---|---|---|---|---|---|
| Pavement | 30.8 | 26.0 | 0.84 | 876 | |
| Structures | Bridges | 13.4 | 8.5 | 0.63 | 187 |
| Culverts | 0.6 | 0.3 | 0.61 | 6 | |
| Subtotal | 14.0 | 8.8 | 0.63 | 193 | |
| Buildings | 1.2 | 0.9 | 0.75 | 20 | |
| Total | 46.0 | 35.7 | 0.78 | 1,089 | |
This example presents a transit agency, located in the Western U.S., termed “The Western Agency.” The agency operates three different transit modes: buses; paratransit vehicles (also called “cutaways”); and a Light Rail Transit (LRT) system. The agency’s asset hierarchy is summarized in Figure 9-6. Major asset classes include revenue vehicles, equipment (service vehicles), facilities and infrastructure. Each of these asset classes consists multiple subclasses. The infrastructure asset class includes the largest number of subclasses. In addition to LRT track, which may be either tangent (straight) or curved, this class includes bridges, special trackwork (grade crossings and switches), and power assets (catenary wire segments, relay cases, and substations).

Previously the Western Agency reported asset value in its TAMP based on the historic cost of asset acquisition or construction. This approach was used to maintain consistency with the agency’s reporting of asset value in its financial statements. As part of the previous effort, the agency collected data on the historic cost and year of purchase or construction for each of the asset classes and subclasses in the TAMP. For revenue vehicles, equipment and facilities costs are tracked at the asset level. For infrastructure assets, costs are tracked by asset subclass, grouping all assets of a given subclass built at a similar time.
For its next TAMP, the agency seeks to report value based on current replacement cost rather than historic cost, as current replacement cost is more closely tied to the cost of rehabilitating and replacing assets. However, for now the agency intends to include both the historic cost of its assets and the current depreciated replacement cost to facilitate comparison with the values in its prior TAMP.
The following subsections describe the approach the agency used for the asset value calculation, followed by a summary of the results. The asset classes are combined into two groups in the discussion: vehicles, which includes revenue vehicle and equipment; and fixed assets, including facilities and infrastructure.
Revenue Vehicles and Equipment (Service Vehicles)
As described above, the agency seeks to establish initial value based on current replacement cost. The agency estimates this initial value by adjusting the historic cost paid for each vehicle for inflation. The agency estimates the annual inflation rate for revenue and service vehicles has historically been approximately 1.6 percent.
The agency next reviews its treatment strategy for vehicles. The agency has established the useful life for its vehicles by vehicle type assuming that planned maintenance and rehabilitation activities are performed on a vehicle over its useful life. The useful life shown in Table 9-2 is estimated based on historical asset performance. At the end of a vehicle’s useful life the vehicle is replaced with a new vehicle. Since vehicle treatments are included within the useful life estimates, the agency establishes that the only treatment explicitly modeled in the asset value calculation should be the initial purchase of the vehicle. While the agency auctions used assets at the end of their useful life, the value received is negligible, so for the sake of this analysis, they assume a residual value of $0. To depreciate vehicle asset value the agency elects to use an age-based approach. The depreciation calculation is made separately for each vehicle.
Table 9-2. Useful Life for Vehicles
| Asset Class | Subclass | Useful Life (years) |
|---|---|---|
| Revenue Vehicles | Buses | 14 |
| Light Rail Vehicles | 40 | |
| Paratransit Vehicles | 10 | |
| Equipment (Service Vehicles) | Automobiles | 8 |
| Steel Wheeled Vehicles | 25 | |
| Trucks and Other Rubber-Tired Vehicles | 14 |
Facilities and Infrastructure
As in the case of vehicles, the agency seeks to establish initial value based on current replacement cost. The agency estimates this initial value by adjusting the historic construction costs of each asset for inflation. The agency estimates the annual inflation rate for construction has been approximately 3.0 percent over the facilities’ lifespan.
Next, the agency reviews its treatment strategies for fixed assets. For these assets, the agency periodically measures asset conditions using the five-point condition scale established by FTA. Using this scale, condition ranges from 1 (worst condition) to 5 (best condition). If an asset has a condition of 2 or less it is deemed to be not in good repair and beyond its useful life. Useful lives are established by asset class, as shown in Table 9-3. When an asset has reached the end of its useful life it is replaced. The agency performs different treatments on an individual asset over its life, but these are reflected in its condition score. Given the availability of condition data, the agency establishes that the only treatment explicitly modeled in the asset value calculation is the asset construction. The agency further assumes that the residual value of an asset at the end of its life is $0.
Table 9-3. Useful Life for Fixed Assets
| Asset Class | Subclass | Useful Life (years) |
|---|---|---|
| Facilities | Administrative | 60 |
| Maintenance | ||
| Public Facilities | ||
| Infrastructure | LRT Track - Tangent | 35 |
| LRT Track - Curved | 30 | |
| LRT Bridges | 70 | |
| Grade Crossings | 15 | |
| Switches | 25 | |
| Catenary Wire Segments | 25 | |
| Relay Cases | 50 | |
| Substations | 25 |
To depreciate asset value the agency elects to use condition-based approach assuming that the change in condition is proportional to age. The effective age of an asset as a function of condition is modeled as follows:
\begin{align*} E(c) &= \frac{UL (5-c)}{(5-2)} \end{align*}
where E(c) is the useful life for a given condition c and UL is the useful life. The denominator is represented by the condition rating at the end of the asset’s useful life subtracted from the highest possible condition rating. With this approach, the effective life of an asset is 0 if its condition is rated as a 5 and is equal to its total useful life if the rating is 2 and it is fully depreciated.
Results Summary
Table 9-4 summarizes the results of the asset value calculation. For each asset class and subclass, it displays the historic cost, replacement cost, current value, ACR and annual depreciation. The table shows that the historic cost of the agency’s assets is $3.1 billion. Adjusting the historic costs for inflation, the current replacement cost of the asset inventory is estimated to be approximately $4.5 billion. The current value, which incorporates depreciation, is approximately $2.7 billion. The ACR for the agency’s asset inventory is 0.60, equal to the current value divided by the replacement cost. Absent investment in the assets, the inventory is expected to depreciate approximately $123 million per year.
Table 9-4. Summary Results for the Western Agency
| Asset Class | Asset Subclass | Historic Cost ($M) | Replacement Cost ($M) | Current Value ($M) | Annual Depreciation ($M) | ACR |
|---|---|---|---|---|---|---|
| Revenue Vehicles | Bus | 456 | 498 | 298 | 34 | 0.60 |
| Light Rail Vehicle | 506 | 603 | 433 | 15 | 0.72 | |
| Paratransit | 25 | 26 | 17 | 3 | 0.65 | |
| Subtotal | 987 | 1,127 | 748 | 51 | 0.66 | |
| Equipment | Automobiles | 3 | 3 | 1 | 0 | 0.27 |
| Steel Wheeled Vehicles | 2 | 2 | 2 | 0 | 0.86 | |
| Trucks and Other Rubber-Tired Vehicles | 35 | 39 | 23 | 3 | 0.60 | |
| Subtotal | 40 | 44 | 26 | 3 | 0.59 | |
| Facilities | Administrative | 19 | 39 | 23 | 1 | 0.58 |
| Maintenance | 170 | 400 | 195 | 7 | 0.49 | |
| Public Facilities | 925 | 1,485 | 789 | 25 | 0.53 | |
| Subtotal | 1,114 | 1,924 | 1,007 | 32 | 0.52 | |
| Infrastructure | LRT Track - Tangent | 503 | 710 | 473 | 20 | 0.67 |
| LRT Track - Curved | 144 | 203 | 135 | 7 | 0.67 | |
| LRT Bridges | 190 | 268 | 161 | 3 | 0.60 | |
| Grade Crossings | 4 | 6 | 3 | 0 | 0.57 | |
| Switches | 4 | 5 | 3 | 0 | 0.50 | |
| Catenary Wire Segments | 35 | 50 | 26 | 2 | 0.53 | |
| Relay Cases | 65 | 87 | 70 | 2 | 0.80 | |
| Substations | 34 | 46 | 28 | 2 | 0.60 | |
| Subtotal | 980 | 1,374 | 899 | 37 | 0.65 | |
| Total | 3,121 | 4,469 | 2,680 | 123 | 0.60 | |
In this example, a state department of transportation in the Midwest, labeled the “Midwest DOT,” applies the economic value approach to quantify benefits realized by users of the state’s primary roadway network. For this example, the state’s primary roadway network is defined as all state-owned Interstates, primary arterials, minor arterials, and major collectors. This example follows the economic approach described in Chapter 4 to estimate the benefits of the primary roadway system. The example provides a better understanding of the value generated by the roadways for direct users and society as a whole. This example shows how state DOTs can estimate the value assets provide to users as compared to the replacement value method, which focuses on what those assets cost.
Application of Economic Value Approach
This case study includes the following basic steps:
- First, traffic data were collected on the Midwest DOT’s primary roadway network. This included all Interstates, principal arterials, minor arterials, and major collectors.
- Second, fatality and serious injury crash rates were collected. These data are maintained by the Midwest DOT and available at the state level.
- Third, emissions rates for the state were collected from the Environmental Protection Agency (EPA) MOVES model. A representative county was selected to generate emissions rates specific to the state.
- Fourth, these data were used to calculate user benefits for the value of travel time, vehicle operating costs, safety, and emissions.
- Fifth, the research team examined the model to interpret the results and found that users of the roadway network experience a much higher monetary value of benefits than the Midwest DOT reports in its TAMP as the replacement costs of the system.
These steps are detailed in the following subsections. A theoretical discussion of the approach is presented at the end of the case study.
Data Collection
The Midwest DOT reports traffic data annually to the Federal Highway Administration (FHWA) as part of its Highway Performance Monitoring System (HPMS) reporting requirements. This data provides a convenient summary of traffic data that can be collected for any state DOT. While 2020 HPMS data was available, this example referenced 2019 HPMS data to avoid any distortions due to restrictions and changed habits during the COVID-19 pandemic. This is consistent with 2021 USDOT guidance for federal discretionary grants, which noted that 2019 traffic data should be used rather than non-representative 2020 data (48).
The analysis utilized the following HPMS variables that were provided by the Midwest DOT:
- Route_ID – This variable is assigned to each individual roadway segment. This identification number is alpha-numeric and contains information on roadway direction, type, and location.
- Section_Length – This variable refers to the length, in miles, of each identified roadway segment. This variable was used, in part, to calculate vehicle-miles traveled (VMT) and vehicle-hours traveled (VHT). These two variables were the basis for estimating all benefits categories included in the analysis.
- F_System – This variable indicates the classification of the system and is broken into seven different types. Segments classified as 1, 3, 4, and 5 were isolated as those correspond with Interstates, principal arterials (other), minor arterials, and major collectors, respectively. Roadways classified as 2, 6 and 7—principal arterials (other freeways and expressways), minor collectors, and local roads, respectively—were not included in the analysis because they are not part of the principal roadway system and did not have a significant number of observations in the dataset.
- Facility_Type – This variable refers to the operational characteristic of the roadway. This variable is important to account for the correct mileage and average annual daily traffic (AADT). Most Interstate segments and many principle arterial segments are separated directionally. The codes used for this variable are as follow:
- 1 – One-way roadway
- 2 – Two-way roadway
- 3 – Couplet
- 4 – Ramp
- 5 – Non-mainline
- 6 – Non-inventory direction
- 7 – Planned/unbuilt
In the HPMS database, many separated Interstates and principal arterials are reported as bidirectional AADT for each separated direction of roadway, so the same bidirectional AADT is reported as Facility_Type 1 in the eastbound direction of a roadway and as Facility_Type 6 in the westbound direction. In order to avoid double-counting of AADT, roadway segments classified as “Non-inventory direction,” or Facility_Type 6, were excluded from this analysis.
- Ownership – This variable indicates the entity that has legal ownership of a roadway and is typically used for apportionment, administrative, legislative, analytical, and national highway database purposes and in cost allocation studies. This example only considers segments with Ownership code 1, which refers to roadways owned by the State DOT.
- Urban_Codes – This variable refers to the U.S. Census Urban Area Code and is used for the querying and analyzing data by the unique identification of a state’s urbanized areas and generically by small urban or rural areas. For this example, the values of urban and rural travel are separated. All segments coded as 99998 or 99999 were considered rural and all others were considered urban.
- AADT – This variable provides the bi-directional annual average daily traffic counts of all vehicles and trucks traveling on the roadway. This variable was used, in part, to calculate VMT and VHT. As discussed above, the “Facility_Type” variable was used in combination with AADT to ensure that bi-directional AADT is not “double counted” in the case of divided or separated roadways.
- AADT_Combination – This variable provides the bi-directional annual average daily traffic counts for combination trucks. Trucks have different operating costs, emission rates, and values of time, so these vehicles are treated separately from passenger vehicles in the analysis. This variable was used, in part, to calculate VMT and VHT as discussed further below.
- AADT_Single_Unit – This variable provides the bi-directional annual average daily traffic counts for single-unit trucks. Trucks have different operating costs and emission rates, and their value of time is calculated differently, so these vehicles are treated separately from passenger vehicles in this analysis. This variable was used, in part, to calculate VMT and VHT.
- Speed Limit – This variable reports the posted speed limit for every roadway segment. The Midwest DOT advised that due to negligible congestion statewide, the research team should use this as the measure for speed of travel. This variable was used, in part, to calculate the VHT of vehicles.
To summarize, roadway segments were sorted to include only those that are Midwest DOT-owned and classified as F_System type Interstate, principal arterial, minor arterial, or major collector. This calculation did not include minor collectors and local roads. Further, segments identified as non-inventory direction under the Facility_Type variable were excluded to prevent any double counting of AADT.
For each F_System type, VMT was calculated separately for urban and rural areas as identified by their Urban Codes. VMT was also calculated separately for passenger vehicles and trucks and aggregated along the criteria stated. The basic calculations for VMT are found below. Note that these calculations represent the VMT calculation for each individual segment. Total VMT is the sum of VMT for all roadway segments, calculated for Interstates, principal arterials, minor arterials, and major collectors and separately for urban and rural areas.
- Passenger Vehicle VMT = [Total Vehicles (AADT) – Total Trucks (AADT_Combination + AADT_Single_Unit)] * Section Length
- Truck VMT = [Total Trucks (AADT_Combination + AADT_Single_Unit)] * Section Length
VMT and speed limits were used to calculate VHT for the same roadway segment criteria. Total passenger vehicle and truck VHT were calculated by summing the VHT from each roadway segment. To calculate VHT, passenger vehicle and truck VMT for each segment was divided by the posted speed limit (in miles-per-hour), which was used as a proxy for average travel speed for this exercise. Typically, observed average travel speeds or VHT collected by the state or calculated using traffic modeling software would be preferable as a measure of vehicle speed, but in this instance the relevant roadways had sufficiently low to nonexistent congestion levels, so speed limit was used as an acceptable measure. The general calculation for passenger vehicle and truck VHT can be found below. Note that this is the VHT calculation for each individual segment. Total VHT would be the summed total of all the roadway segments.
- Passenger Vehicle VHT = Segment Passenger Vehicle VMT / Segment Speed Limit
- Truck VHT = Segment Truck VMT / Segment Speed Limit
User Cost Calculation
In the next step, monetary values were applied to the VMT and VHT aggregations to calculate the user benefits (or in this case, user costs) associated with willingness-to-pay for travel time, vehicle operating costs, safety, and emissions. This analysis utilized monetization parameters recommended per the United States Department of Transportation (USDOT) Benefit-Cost Analysis Guidance for Discretionary Grant Programs as of February 2021 (48).
Travel Time
USDOT guidance recommends a value of time for passengers and truck drivers of $17.90 and $30.80 per hour, respectively. Passenger vehicles are assumed to have 1.67 occupants and trucks are assumed to have one occupant. The basic calculations for the value of travel time for passenger vehicles and trucks used in this analysis can be found below:
- Total Value of Travel Time for Passenger Vehicles = $17.90 * 1.67 occupants * Total Passenger Vehicle VHT
- Total Value of Travel Time for Trucks = $30.80 * 1 occupant * Total Truck VHT
Vehicle Operating Cost
USDOT guidance recommends a per-mile vehicle operating cost of $0.43 for passenger vehicles and $0.93 for trucks. These values were applied directly to the VMT calculated for passenger vehicles and trucks. The basic calculations for the value of vehicle operating costs used in this analysis can be found below:
- Total Value of Passenger Vehicle Operating Costs = Total Passenger Vehicle VMT * $0.43
- Total Value of Truck Operating Costs = Total Truck VMT * $0.93
Safety
USDOT guidance recommends a monetized value of an averted fatality of $10,900,000 and a monetized value of an averted injury (of unknown severity) of $197,600. The Midwest DOT provided crash rates by severity and facility type for rural and urban areas in its Highway Safety Improvement Program (HSIP). These rates are reported as incident rates per hundred-million vehicle miles traveled (HMVMT). The basic calculations for the value of safety incidents used in this analysis can be found below:
Fatality Crashes
- Total Value of Passenger Vehicle Fatal Crashes = [Total Passenger Vehicle VMT / 10^6] * $10,900,000 * Fatal crash rate per HMVMT
- Total Value of Truck Fatal Crashes = [Total Truck VMT / 10^6] * $10,900,000 * Fatal crash rate per HMVMT
Injury Crashes
- Total Value of Passenger Vehicle Injury Crashes = [Total Passenger Vehicle VMT / 10^6] * $197,600 * Injury crash rate per HMVMT
- Total Value of Truck Injury Crashes = [Total Truck VMT / 10^6] * $197,600 * Injury crash rate per HMVMT
Emissions
USDOT recommends emissions valuations per metric ton of pollutant emitted by pollutant type and year. These monetized values are applied to pollutant quantities calculated using the EPA MOVES model for a representative county in the state. The MOVES model reports grams of pollutant emitted per mile driven. It has separate emissions rates for passenger vehicles and trucks, urban and rural roadways, and various speed bins which consider the different fuel efficiency experienced at different speeds. Below are the monetized values per metric ton of pollutant emitted by type and year.
Table 9-5. Cost per Metric Ton of Pollutant from the MOVES Model
| Emission Type | NOx | SO2 | PM2.5 | CD2 |
|---|---|---|---|---|
| 2020 | $15,700 | $40,400 | $729,300 | $50 |
| 2021 | $15,900 | $41,300 | $742,300 | $52 |
| 2022 | $16,100 | $42,100 | $755,500 | $53 |
| 2023 | $16,400 | $43,000 | $769,000 | $54 |
| 2024 | $16,600 | $43,900 | $782,700 | $55 |
| ... | ... | ... | ... | ... |
| 2050 | $18,000 | $48,200 | $852,700 | $84 |
The basic calculation for the value of emissions used in this analysis can be found below:
- Total Value of Passenger Vehicle Emissions = Total Passenger Vehicle VMT * [Grams of Pollutant Emitted by Type / 1000^2] * Monetary Value of Pollutant by Type
- Total Value of Truck Emissions = Total Truck VMT * [Grams of Pollutant Emitted by Type / 1000^2] * Monetary Value of Pollutant by Type
The value of emissions is dependent on the year in the analysis so annual emissions should be calculated for each year and applied to that specific year’s monetary value.
Analysis Period and Discounting
This exercise used a 20-year analysis period, which is consistent with USDOT BCA guidance. The beginning year for values was set at 2020 and concluded in 2039 to cover a 20-year period. In accordance with USDOT guidance, all monetized values were discounted at 7 percent with the exception of values related to carbon dioxide emissions, which were discounted at 3 percent. The general formula for calculating the discount rate can be found below:
- Discount Rate = 1 / [(1 + Discount Rate) ^ (Year of Analysis – Base Year of Analysis)]
Discounted benefits for each year were aggregated to calculate the discounted total benefits realized by the state’s primary roadway network over the analysis period. Because the benefits were calculated separately by F_System type and for urban and rural areas the total benefits can be viewed with added levels of granularity as needed.
Results of Economic Value Approach
This example reveals significant value in the state’s primary roadway network. Annual travel recorded in 2019 was projected with no assumed growth rate for each year of the analysis period. The value experienced by roadway users in Year 1 of the analysis was calculated at $13.2 billion. Over a 20-year time period this equates to $258.7 billion in undiscounted terms or $148.0 billion when discounted at 7 percent (3 percent for carbon dioxide emissions). The most significant drivers of value were travel time and vehicle operating costs, which were $5.7 billion and $6.1 billion (annually), respectively.
Table 9-6. Summary of the Midwest Agency’s Roadway Network Value
| User Cost Category | Single-Year Value ($B) | 20-Year Value Undiscounted ($B) | 20-Year Value Discounted at 7% (3% for CO2) ($B) |
|---|---|---|---|
| Travel Time | $5.74 | $114.79 | $65.06 |
| Vehicle Operating Costs | $6.05 | $121.02 | $68.59 |
| Traffic Safety | $0.71 | $14.10 | $7.99 |
| Emissions | $0.66 | $8.75 | $6.31 |
| Total | $13.16 | $258.66 | $147.95 |
The single year value experienced by the roadway is roughly half of the network’s total replacement value as reported in the Midwest DOT’s Transportation Asset Management Plan. This implies that after approximately two years of use the roadway network has already provided value to the public equal to the entire replacement cost of the network. A significant portion of the state’s travel occurs on the primary network and this is reflected in the significant value experienced by users.
Overall, the value realized in urban areas ($7.1 billion annually) is slightly greater than that realized in rural areas ($6.1 billion annually).
Table 9-7. Single Year Value for Urban and Rural Roads at the Midwest Agency.
| User Cost Category | Urban Single-Year Value ($B) | Rural Single-Year Value ($B) | Total Single-Year Value ($B) |
|---|---|---|---|
| Travel Time | $3.39 | $2.35 | $5.74 |
| Vehicle Operating Costs | $3.00 | $3.05 | $6.05 |
| Traffic Safety | $0.41 | $0.30 | $0.71 |
| Emissions | $0.25 | $0.41 | $0.66 |
| Total | $7.06 | $6.10 | $13.16 |
At the state level, Interstates account for $9.9 billion in annual value, principal arterials account for $3.2 billion, minor arterials account for $0.04 billion, and major collectors account for $0.02 billion. For the Interstate system alone, the rural annual value ($6.05 billion) exceeds urban annual value ($3.8 billion). Approximately 99 percent of the total value of Midwest DOT rural roadways is on the Interstates, with only $45 million of rural annual value coming from principal arterials, minor arterials, and major collectors. Principal arterials represent a much larger share of value in urban areas.
Overall, Interstates account for 75.0 percent of value, principal arterials account for 24.5 percent, and combined minor arterials and major collectors account for the remaining 0.5 percent.
Table 9-8. Single Year Value for Each Road Category at the Midwest Agency.
| User Cost Category | Interstate Single-Year Value ($B) | Principal Arterial Single-Year Value ($B) | Minor Arterial Single-Year Value ($B) | Major Collector Single-Year Value ($B) | Total Single-Year Value ($B) |
|---|---|---|---|---|---|
| Travel Time | $4.05 | $1.67 | $0.02 | $0.01 | $5.74 |
| Vehicle Operating Cost | $4.79 | $1.24 | $0.02 | $0.01 | $6.05 |
| Traffic Safety | $0.47 | $0.23 | $0.01 | $0.00 | $0.71 |
| Emissions | $0.57 | $0.09 | $0.00 | $0.00 | $0.66 |
| Total | $9.87 | $3.23 | $0.04 | $0.02 | $13.16 |
It is clear that the Midwest DOT’s primary roadway network generates significant user value in the state. The value generated in a single year equates to roughly half the total replacement cost as reported in the Midwest DOT’s TAMP annually. This highlights the high value the Midwest DOT creates by simply maintaining the existing infrastructure. The service life of roadways extends well beyond the payback period and generates value many times over the replacement cost in both discounted and undiscounted terms. The primary roadway network is an important societal and economic asset in the state worth far more to its users than is captured by the replacement cost approach.
Theoretical Framework of Economic Approach Example
This example applied the economic value approach to assess the value of the Midwest DOT’s primary roadway network. The implementation of such a system-wide assessment is challenging to conduct using the economic value steps described in Chapter 4, because it is difficult in practice to identify what the “next best alternative road class” would be relative to the entire state-owned roadway network.
On a smaller scale, such as that of an individual roadway improvement project, economic value can be assessed by comparing projected user costs with and without the infrastructure (e.g., bridge or roadway segment) being considered. However, in a system-wide assessment (e.g., for the entire state highway network), the with and without project contexts cannot be evaluated because travel behavior would be fundamentally different without the highway system. Trying to run a travel demand model without the state highway system would produce extreme results that do not reflect how society or travel would operate without the state highway system.
Given these limitations, this example assesses economic value as the sum of all observed user costs incurred for travel along the Midwest DOT’s primary roadway network. The theoretical basis of this valuation exercise can be explained by considering the value of an individual trip. If an individual chooses to travel from point A to point B and incur all the associated costs of doing so, then the overall value of that trip to the individual must at least be equal to the total costs incurred by the individual over the course of the trip. If the trip costs more to the individual than it is worth, that persons will not make the trip. Put another way, an individual will choose to travel along infrastructure only when the value realized is greater than (or potentially equal to) the cost of travelling. Accordingly, one can calculate the minimum value of a trip by monetizing the cost of the trip.
This theoretical approach can be expanded beyond an individual trip and applied to all trips across a roadway network. The aggregate value to society of all travel on a roadway network must at least be equal to the sum of all user costs incurred for travel on that roadway network. These total user costs include vehicle operating costs, value of travel time, monetized emissions costs, and injury and fatality crash costs.
Observed User Costs versus Willingness-to-Pay
The theoretical framework that underlies this example is related to the economic concept of “willingness-to-pay.” If a user is willing to pay a maximum of x dollars for a good, then that good must be worth x dollars to the individual. If the individual has the opportunity to purchase the good for any amount up to x dollars then a rational person will make that purchase, but if the cost of the good is above x then a rational person will choose not to purchase the good.
While willingness-to-pay reflects value, this value can be difficult to measure in practice. Willingness-to-pay for any given good varies greatly across individuals, but the prices of goods are much more standardized. Accordingly, most market transactions end up being made at a price below maximum willingness-to-pay for any given purchaser. An individual may be willing to pay up to x dollars for a good, but the person is likely in practice to find a price below x dollars for the goods that purchase. This is the case in using the user costs to estimate the value of travel in the Midwest DOT example.
While the amount paid (or costs incurred) for travel can be measured using the data available in this example, total willingness-to-pay cannot be assessed. The available data can be used to calculate what users do pay for travel, but it cannot be used to show what users would be willing to pay if travel were more expensive. As total willingness-to-pay reflects value and amount paid must be no greater than, and is often less than, willingness-to-pay, it follows that total amount paid is an underestimate of total value. Thus, the observed cost of all travel on the state’s primary roadway network reflects a “floor”—or a conservative understatement—of the total value of travel, and the actual value of travel realized across the roadway network must exceed this cost on the societal level. The exact extent to which actual value exceeds aggregate user costs depends on the economic concept of “elasticity of demand” for travel, which cannot be assessed in this example.
Implications of Measuring Observed User Costs (versus Willingness-to-Pay)
Since user costs represent a minimum user value, the implication of the economic value approach is that a decrease in travel costs within the state could appear to represent a decrease in value of the Midwest DOT’s infrastructure. For example, a hypothetical improvement to roadway conditions that leads to faster travel times, lower emissions, or safer roadway conditions would result in lower per-user travel costs being borne by users. Under an assumption of relatively inelastic demand, this decreased per-user travel cost would also result in lower aggregate observed travel costs across the state. Using the economic value approach, this improvement in roadway conditions would apparently decrease the value of the roadway, as the lower aggregate travel cost would reflect an apparent lower economic value of infrastructure. This seemingly contradictory finding—infrastructure that is more beneficial to its users should have greater economic value, not less—is a result of the data limitations that restrict the analysis to measuring only the observed travel costs borne by users (which were reduced in this example) rather than their true willingness-to-pay for travel.
While a roadway condition improvement may decrease the cost of travel along a route, it does not decrease willingness-to-pay for that travel. Thus, the lower user costs resulting from the improvement project will widen the “gap” between willingness-to-pay and cost borne. Total value realized by users will not change for all those pre-existing users of the facility, and any additional users who choose to use the facility as a result of the improvement project will realize additional value. Thus, while the lower per-user cost may appear to reflect lower economic value of infrastructure, it really represents a more conservative estimate of user value, which remains unchanged.
Limitations
There are at least four additional limitations to the analysis conducted in this case study:
- Internalization of emissions costs and crash risk – This example included vehicle operating costs, value of travel time, monetized emissions costs, and injury and fatality crash costs as observed user costs of travel. However, emissions costs and safety risk may not be fully “internalized” by users. That is, do individuals who make choices to travel on roads fully appreciate the crash risk associated with their travel and do they fully bear the societal costs of the emissions from their vehicles? If these costs are not fully “internalized” by the travelers, then it may be inappropriate to consider those costs as a component of “willingness-to-pay” for travel.
- Fixed travel costs – This example considers the marginal cost per-mile and per-hour of travel but does not consider the fixed (or sunk) costs also required for travel. Annual vehicle ownership costs, for example, do not directly depend on distance traveled per year. Thus, monetizing the revealed marginal cost of travel on a per-mile or per-hour basis understates the total cost of travel on an annual basis, and accordingly understates the total willingness-to-pay for travel.
- Roadway maintenance expenses – An additional cost of travel borne by society is the cost of construction, maintenance, and upkeep of public infrastructure. Some, but not all, of this cost is incorporated in user expenses, such as gasoline taxes and tolls. To capture the observed user costs of travel fully, it would be necessary to account for all roadway construction, maintenance, and upkeep expenses. However, these expenses cannot fully be captured using available data and applied to per-mile or per-vehicle parameter estimates.
- Apportionment of the value of travel – A challenge in applying willingness-to-pay theory to the valuation of roadway infrastructure is apportioning the overall value of travel among different components necessary for travel. For example, travel along an Interstate requires the Interstate infrastructure, but it also requires a vehicle and a source of fuel. Interstate travel cannot happen if any one of these multiple required inputs is unavailable. It would therefore be inappropriate to apportion the total value of Interstate travel to the Interstate infrastructure itself, as this would leave no value for the vehicle and fuel that are also required for travel. The willingness-to-pay theory behind this example does not provide insight as to what percentage of the overall value of travel should be apportioned to the roadway itself, versus what should be apportioned to other inputs required for travel.
This section describes cases studies profiling the asset valuation approaches of two highway agencies from Britain and Australia. Each case study demonstrates how the agency defines its asset hierarchy, establishes replacement costs, and calculates depreciation. The agencies profiled in the case studies follow the asset valuation guidance established in their respective countries, and their work in this area predates the development of this document. Nonetheless, both agencies use approaches that are very consistent with the guidance presented here, illustrating the common philosophy between the guidance, international standards for calculating asset value, and the state of the practice worldwide.
Highways England is a public company responsible for managing the Strategic Road Network (SRN) in England, which is a core set of 4,300 miles of major roads that represents a third of all road traffic and two thirds of freight traffic. The organization is wholly owned by the British government and receives all of its capital and revenue funding directly from the United Kingdom (UK) Department for Transport (DfT). Nonetheless, Highways England operates as a company, and produces company financial accounts to provide visibility of its ongoing stewardship and value in terms of taxpayer equity. Asset value is computed and reported as part of the organization’s financial health.
The following paragraphs describe the approach used by Highways England to value its portion of the total British SRN. Note that Highway England’s approach is also used by the other SRN operating organizations: Transport Scotland for the SRN in Scotland; the Welsh Government for the SRN in Wales; and the Northern Ireland Department for Infrastructure for the SRN and all local roads in Northern Ireland. Additionally, the Northern Ireland Department for Infrastructure uses the same methodology for river and coastal assets in Northern Ireland.
Highways England’s approach to asset valuation is undertaken in accordance with Government Financial Reporting Manual (FReM) (49). For infrastructure assets, the manual uses the principles of Royal Institution of Chartered Surveyors (RICS) as described in the RICS “Red Book” (50). The company determines the fair value of the SRN using Depreciated Replacement Cost (DRC) in accordance with the guidance provided by the FReM and the Red Book. This approach is consistent with accounting standard IFRS 13 for calculating fair value (3). It results in the calculation of the value of the SRN from the perspective of a theoretical buyer based on how much it would cost to construct a network of equivalent service potential.
Figure 9-7 summarizes the process used by Highways England for calculating value. First, the organization calculates capital expenses. These costs are adjusted to obtain the ‘as new’ replacement cost based on a modern equivalent asset offering the same function (which the company establishes as identical routing and capacity) on a greenfield site.
Replacement costs are calculated for four asset classes:
- Pavements;
- Structures;
- Technology Assets; and
- Land
Note that the valuation for pavement is assumed to include the value of a number of other ancillary assets, such as vehicle restraint systems, signage, drainage, and other traffic and safety assets. For each asset class Highways England first calculates unit rates, and then applies the unit rate to the asset quantity to calculate replacement cost.
Following the calculation of replacement cost, the organization then calculates depreciation. Depreciation and other adjustments account for impaired or obsolete (derecognized) assets and are applied to the replacement cost to obtain DRC. Depreciation of asset value is calculated based upon asset condition surveys. While renewals are performed that improve conditions, these are not treated for accounting purposes as having an impact upon the valuation of the network because any related improvement in road condition are reflected in the condition surveys. Thus, Highways England depreciate 100% of renewals expenditures in the year that they are incurred.
Depreciation is based on the observed condition of assets. For pavement, condition is measured based on rutting. For structures, an Element Condition Score is obtained from structure inspections performed for each element of a structure. Land assets are not depreciated.
To ensure a robust valuation, Highways England undertakes a full valuation of each asset category at intervals not exceeding five years. A revaluation of pavements and lands was undertaken in the period of 2019 to 2020. At the time of that valuation, the value of the SRN was estimated to be approximately £123.2 billion. Updated valuations of structures and technology are planned in 2023 and 2024, respectively.
Highways England makes improvements to its valuation approach on a continuing basis. For example, historically depreciation for pavement is calculated based on rutting. In the future, Highways England plans to improve this depreciation calculation by including other pavement distresses, such as fretting, texture, and longitudinal cracking. Also, the organization plans to perform a separate calculation for special structures, unique to the network, that are best valued on a case-by-case basis rather than using unit rates.
This case study describes the asset valuation approach used by a major government road authority in Australia. The authority is responsible for managing a large network of public roads, privately-funded toll roads, bridges, culverts, tunnels, and other assets. Valuations are conducted according to local government and national (Australian) accounting policies and standards. These standards emphasize basing estimates on fair value, consistent with international accounting standards.
The agency uses what it calls “Optimized Depreciated Replacement Cost (ODRC)” to value its assets. This term highlights that the replacement cost used is the cost to replace an asset with its modern equivalent, rather than the cost of a replacing an asset in-kind.
Figure 9-8 summarizes the process used by the authority to calculate fair value for its assets. As shown in the figure, the process includes steps for calculating replacement cost, and then adjusting replacement cost based on deprecation. Note the authority’s process includes some additional steps not shown in the figure which further modify fair value to reflect planned work.
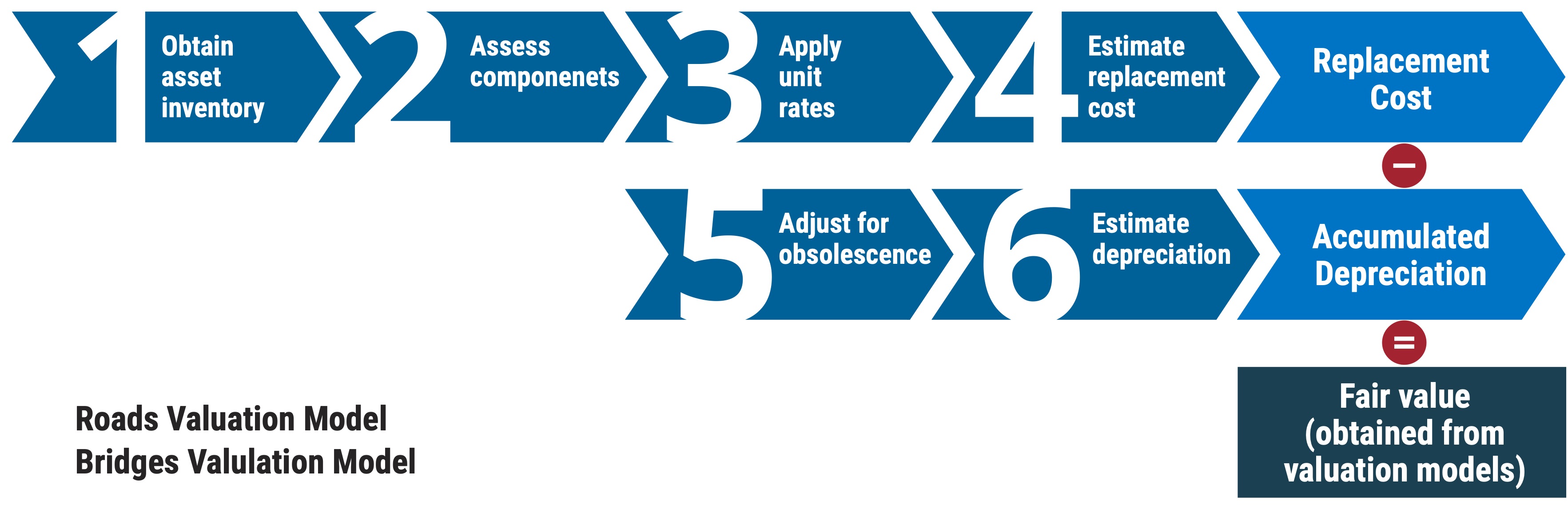
The approach is applied to calculate value for four asset classes: roads; minor roads; bridges; and tunnels. Assets are valued at the component-level where sufficient data are available to support the calculation. Figure 9-9 shows how roads and bridges are subdivided into components.
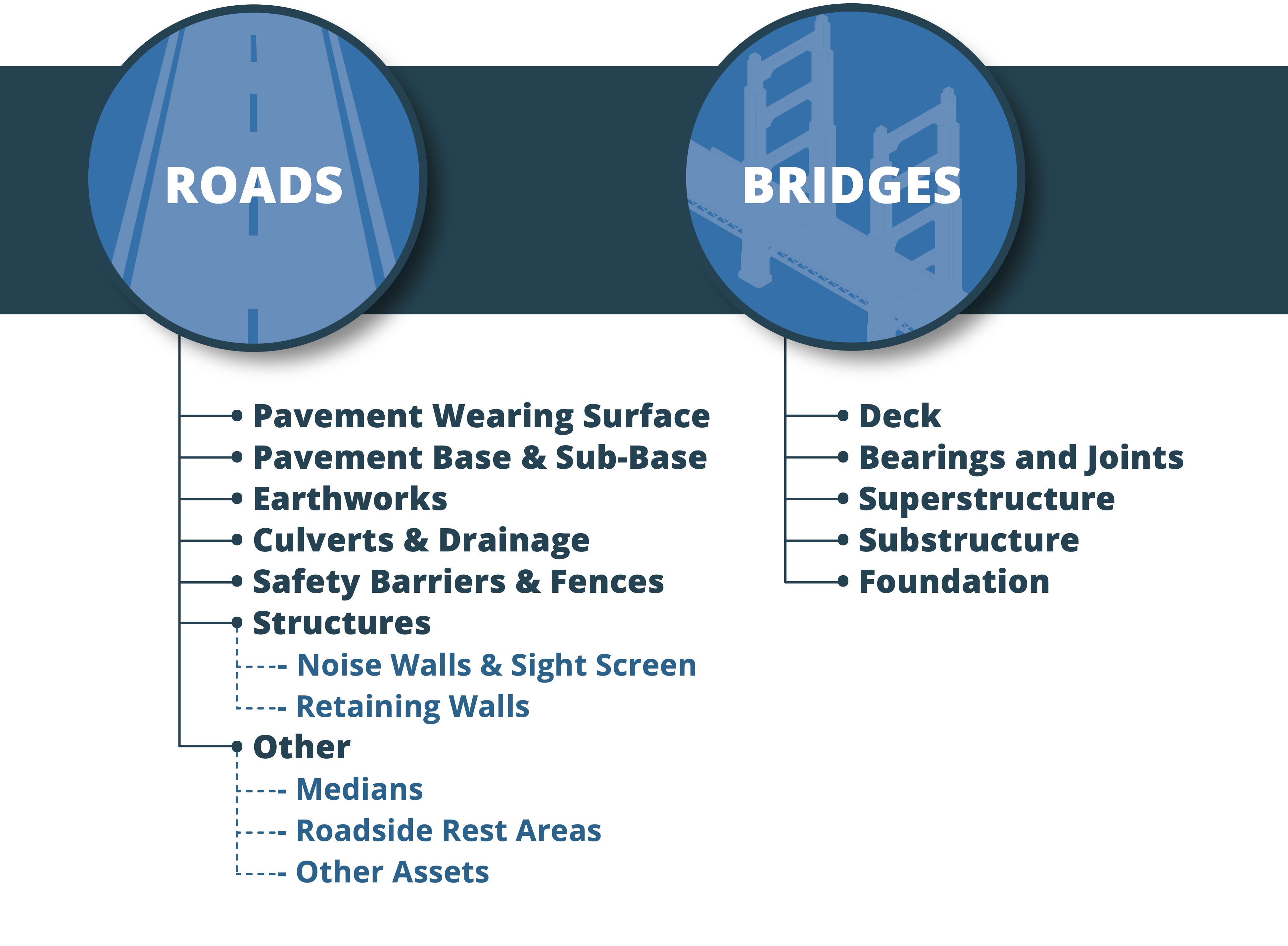
Depreciation is calculated based on condition data where data are available to support the calculation. For example, the authority calculates a measure of pavement condition called Pavement Health Index (PHI) which is based on data for rutting, cracking, and other pavement distresses. Separately the authority performs an analysis to relate PHI to effective age. This relationship is applied to estimate the effective age of each segment, which is subsequently used to calculate depreciation for the pavement wearing surface. Figure 9-10 shows the relationship between PHI and effective age for flexible pavement.
Note that where detailed data are unavailable for a given asset component, the value of the component is estimated as a percentage of the value of the asset. Also, earthwork assets are not depreciated.
The end result of the calculation is an asset value that is comprehensive, leverages detailed data on individual components, and reflects best engineering judgement on asset condition and remaining life.